Exploring the nonlinear geometry of protein homology
- PMID: 12876310
- PMCID: PMC2323947
- DOI: 10.1110/ps.0379403
Exploring the nonlinear geometry of protein homology
Abstract
The explosion of biological data resulting from genomic and proteomic research has created a pressing need for data analysis techniques that work effectively on a large scale. An area of particular interest is the organization and visualization of large families of protein sequences. An increasingly popular approach is to embed the sequences into a low-dimensional Euclidean space in a way that preserves some predefined measure of sequence similarity. This method has been shown to produce maps that exhibit global order and continuity and reveal important evolutionary, structural, and functional relationships between the embedded proteins. However, protein sequences are related by evolutionary pathways that exhibit highly nonlinear geometry, which is invisible to classical embedding procedures such as multidimensional scaling (MDS) and nonlinear mapping (NLM). Here, we describe the use of stochastic proximity embedding (SPE) for producing Euclidean maps that preserve the intrinsic dimensionality and metric structure of the data. SPE extends previous approaches in two important ways: (1) It preserves only local relationships between closely related sequences, thus allowing the map to unfold and reveal its intrinsic dimension, and (2) it scales linearly with the number of sequences and therefore can be applied to very large protein families. The merits of the algorithm are illustrated using examples from the protein kinase and nuclear hormone receptor superfamilies.
Figures
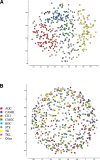

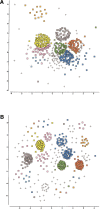


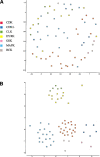
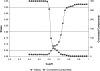

Similar articles
-
A geodesic framework for analyzing molecular similarities.J Chem Inf Comput Sci. 2003 Mar-Apr;43(2):475-84. doi: 10.1021/ci025631m. J Chem Inf Comput Sci. 2003. PMID: 12653511
-
Stochastic proximity embedding.J Comput Chem. 2003 Jul 30;24(10):1215-21. doi: 10.1002/jcc.10234. J Comput Chem. 2003. PMID: 12820129
-
Automatic classification of protein structures using low-dimensional structure space mappings.BMC Bioinformatics. 2014;15 Suppl 2(Suppl 2):S1. doi: 10.1186/1471-2105-15-S2-S1. Epub 2014 Jan 24. BMC Bioinformatics. 2014. PMID: 24564500 Free PMC article.
-
A modified update rule for stochastic proximity embedding.J Mol Graph Model. 2003 Nov;22(2):133-40. doi: 10.1016/S1093-3263(03)00155-4. J Mol Graph Model. 2003. PMID: 12932784
-
Incorporating homologues into sequence embeddings for protein analysis.J Bioinform Comput Biol. 2007 Jun;5(3):717-38. doi: 10.1142/s0219720007002734. J Bioinform Comput Biol. 2007. PMID: 17688313
Cited by
-
Molecular evolution of phosphoprotein phosphatases in Drosophila.PLoS One. 2011;6(7):e22218. doi: 10.1371/journal.pone.0022218. Epub 2011 Jul 15. PLoS One. 2011. PMID: 21789237 Free PMC article.
References
-
- Apostal, I.S. and Szpankowski, W. 1999. Indexing and mapping of proteins using a modified nonlinear Sammon projection. J. Comput. Chem. 20 1049–1059.
-
- Apweiler, R., Attwood, T.K., Bairoch, A., Bateman, A., Birney, E., Biswas, M., Bucher, P., Cerutti, L., Corpet, F., Croning, M.D.R., et al. 2001. The InterPro database, an integrated documentation resource for protein families, domains and functional sites. Nucleic Acids Res. 29 37–40. - PMC - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

