Rethinking the evolutionary theory of aging: transfers, not births, shape senescence in social species

Abstract

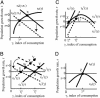
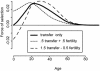
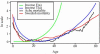
The classic evolutionary theory of aging explains why mortality rises with age: as individuals grow older, less lifetime fertility remains, so continued survival contributes less to reproductive fitness. However, successful reproduction often involves intergenerational transfers as well as fertility. In the formal theory offered here, age-specific selective pressure on mortality depends on a weighted average of remaining fertility (the classic effect) and remaining intergenerational transfers to be made to others. For species at the optimal quantity-investment tradeoff for offspring, only the transfer effect shapes mortality, explaining postreproductive survival and why juvenile mortality declines with age. It also explains the evolution of lower fertility, longer life, and increased investments in offspring.

Fig. 1.

(A) Equilibrium population size and age distribution, reflecting density and intergenerational transfers (see Population Equilibrium with Intergenerational Transfers for details). (B) The effect on r and γ of a mortality-reducing mutation when the balance curve is downward sloping (see Mutation and Selection Without Age). (C) Selection effects on the left of a hump, where the classical effects are reversed. Evolution moves toward the optimal equilibrium at the peak (see The Evolutionary Trajectory to the Optimal Equilibrium). (D) The optimal equilibrium is evolutionarily stable (see The Evolutionary Trajectory to the Optimal Equilibrium).

Fig. 2.

The force of selection on mortality is a weighted average of the fertility effect and the transfer effect (Eq. 6 in Appendix), illustrated for Ache forager–horticulturist data (–37). Short dashes, selection to right of hump; long dashes, selection to left of hump; solid line, selection at peak of hump.

Fig. 3.

Comparison of actual mortality schedules with predicted mortality for classical theory and present theory. Mortality should be inversely proportional to force of selection, so logarithms of age-specific death rates, 1/F(a), and 1/T(a) are shown. Fertility, mortality, and transfers are for Ache (–37). Also plotted is mortality for 18th-century Sweden (data from Human Mortality Database, University of California, Berkeley, and Max Planck Institute for Demographic Research, Rostock, Germany, and available at www.mortality.org or www.humanmortality.de). All curves are adjusted to have the same minimum at 0, because only shape is being compared. Actual juvenile and adult mortalities agree well with the transfer theory and poorly with classical theory.