Metabolic switching in the sugar phosphotransferase system of Escherichia coli
- PMID: 12885625
- PMCID: PMC1303199
- DOI: 10.1016/S0006-3495(03)74517-2
Metabolic switching in the sugar phosphotransferase system of Escherichia coli
Abstract
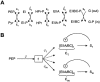
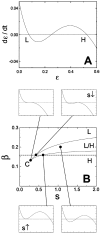
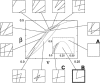
Bacteria grown in a mixture of multiple sugars will first metabolize a preferred sugar until it is nearly depleted, only then turning to other carbon sources in the medium. This sharp switching of metabolic preference is characteristic of systems that optimize fitness. Here we consider the mechanism by which switching can occur in the Escherichia coli phosphotransferase system (PTS), which regulates the uptake and metabolism of several sugars. Using a model combining the description of fast biochemical processes and slower genetic regulation, we derive metabolic phase diagrams for the uptake of two PTS sugars, indicating regions of distinct sugar preference as a function of external sugar concentrations. We then propose a classification of bacterial phenotypes based on the topology of the metabolic phase diagram, and enumerate the possible topologically distinct phenotypes that can be achieved through mutations of the PTS. This procedure reveals that there is only one nontrivial switching phenotype that is insensitive to large changes in biochemical parameters. This phenotype exhibits diauxic growth, a manifestation of the winner-take-all dynamics enforced by PTS architecture. Winner-take-all behavior is implemented by the induction of sugar-specific operons, combined with competition between sugars for limited phosphoryl flux. We propose that flux-limited competition could be a common mechanism for introducing repressive interactions in cellular networks, and we argue that switching behavior similar to that described here should occur generically in systems that implement such a mechanism.
Figures
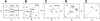


References
-
- Alon, U., M. G. Surette, N. Barkai, and S. Leibler. 1999. Robustness in bacterial chemotaxis. Nature. 397:168–171. - PubMed
-
- Chung, J. D., and G. Stephanopoulos. 1996. On physiological multiplicity and population heterogeneity of biological systems. Chem. Eng. Sci. 51:1509–1521.
-
- Danzig, G. B. 1963. Linear Programming and Extensions. Princeton University Press, Princeton, NJ.
-
- Edwards, J. S., R. U. Ibarra, and B. Ø. Palsson. 2001. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat. Biotechnol. 19:125–130. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

