Optimal design of a bistable switch
- PMID: 12909724
- PMCID: PMC187806
- DOI: 10.1073/pnas.1531507100
Optimal design of a bistable switch
Abstract
Determining optimally designed structures is important for diverse fields of science and engineering. Here we describe a procedure for calculating the optimal design of a switch and apply the method to a bistable microelectromechanical system relay switch. The approach focuses on characterizing the unstable transition state connecting the two stable equilibria to control the force displacements. Small modifications in component shape lead to a substantial improvement in device operation. Fabrication of the optimized devices confirms the predictions.
Figures

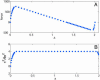
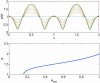


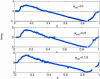
References
-
- Banichuk, N. V. (1983) Problems and Methods of Optimal Structural Design (Plenum, New York).
-
- Bendsoe, M. P. (1988) Comp. Methods Appl. Mech. Eng. 71, 197–224.
-
- Keller, J. B. (1960) Arch. Rat. Mech. Anal. 5, 275–285.
-
- Cox, S. J. (1992) Math. Intell. 14, 16–24.
-
- Keller, J. B. & Niordson, F. I. (1966) J. Math. Mech. 16, 433–446.
LinkOut - more resources
Full Text Sources
Other Literature Sources

