A graph-theory algorithm for rapid protein side-chain prediction
- PMID: 12930999
- PMCID: PMC2323997
- DOI: 10.1110/ps.03154503
A graph-theory algorithm for rapid protein side-chain prediction
Abstract
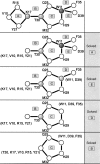
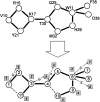
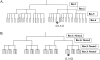
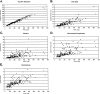
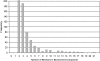
Fast and accurate side-chain conformation prediction is important for homology modeling, ab initio protein structure prediction, and protein design applications. Many methods have been presented, although only a few computer programs are publicly available. The SCWRL program is one such method and is widely used because of its speed, accuracy, and ease of use. A new algorithm for SCWRL is presented that uses results from graph theory to solve the combinatorial problem encountered in the side-chain prediction problem. In this method, side chains are represented as vertices in an undirected graph. Any two residues that have rotamers with nonzero interaction energies are considered to have an edge in the graph. The resulting graph can be partitioned into connected subgraphs with no edges between them. These subgraphs can in turn be broken into biconnected components, which are graphs that cannot be disconnected by removal of a single vertex. The combinatorial problem is reduced to finding the minimum energy of these small biconnected components and combining the results to identify the global minimum energy conformation. This algorithm is able to complete predictions on a set of 180 proteins with 34342 side chains in <7 min of computer time. The total chi(1) and chi(1 + 2) dihedral angle accuracies are 82.6% and 73.7% using a simple energy function based on the backbone-dependent rotamer library and a linear repulsive steric energy. The new algorithm will allow for use of SCWRL in more demanding applications such as sequence design and ab initio structure prediction, as well addition of a more complex energy function and conformational flexibility, leading to increased accuracy.
Figures
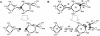


References
-
- Bower, M.J., Cohen, F.E., and Dunbrack Jr., R.L. 1997. Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: A new homology modeling tool. J. Mol. Biol. 267 1268–1282. - PubMed
-
- De Maeyer, M., Desmet, J., and Lasters, I. 1997. All in one: A highly detailed rotamer library improves both accuracy and speed in the modelling of side-chains by dead-end elimination. Fold Des. 2 53–66. - PubMed
-
- ———. 2000. The dead-end elimination theorem: Mathematical aspects, implementation, optimizations, evaluation, and performance. Methods Mol. Biol. 143 265–304. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

