Mathematical model of the spatio-temporal dynamics of second messengers in visual transduction

Abstract

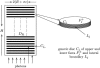
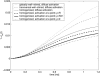
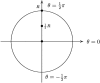
A model describing the role of transversal and longitudinal diffusion of cGMP and Ca(2+) in signaling in the rod outer segment of vertebrates is developed. Utilizing a novel notion of surface-volume reaction and the mathematical theories of homogenization and concentrated capacity, the diffusion of cGMP and Ca(2+) in the inter-disc spaces is shown to be reducible to a one-parameter family of diffusion processes taking place on a single rod cross section; whereas the diffusion in the outer shell is shown to be reducible to a diffusion on a cylindrical surface. Moreover, the exterior flux of the former serves as a source term for the latter, alleviating the assumption of a well-stirred cytosol. A previous model of visual transduction that assumes a well-stirred rod outer segment cytosol (and thus contains no spatial information) can be recovered from this model by imposing a "bulk" assumption. The model shows that upon activation of a single rhodopsin, cGMP changes are local, and exhibit both a longitudinal and a transversal component. Consequently, membrane current is also highly localized. The spatial spread of the single photon response along the longitudinal axis of the outer segment is predicted to be 3-5 microm, consistent with experimental data. This approach represents a tool to analyze point-wise signaling dynamics without requiring averaging over the entire cell by global Michaelis-Menten kinetics.

FIGURE 1

Geometrical description of the ROS and its outer shell.

FIGURE 2

Geometry of the ROS and its discs.

FIGURE 3

Activation by a single R^* with [PDE^*] given by the lumped/bulk model (Eqs. 23a and 23b). History of the relative integrated current J_int. After 800 ms, dark current suppression is ∼1.54% for a well-stirred ROS, ∼1.34% for ROS well stirred in the transversal variables, and ∼0.94% for a fully space-resolved model. Thus, the more space resolved is the model, the less is the current suppression. The three lowest curves represent current suppression for the homogenized model activated by a punctual source as in Eq. 24. The three activation sites are in Fig. 4. Current suppression is dramatically dependent on the activation site.

FIGURE 4

Transversal cross section of the rod outer segment at the level z_o of the disc where activation occurs. Activations are simulated at 0, at and and on the boundary of the rod at R and

FIGURE 5

Plots of 1 − J_rel(z, t) at times 0.2, 0.4, 0.6, 0.8, 1.2 s. (A, B) Activation by Eqs. 23a and 23b. (A) Model with ROS well stirred in the transversal variables; spr(0.6 s) = 3.28 μm; spr(1.2 s) = 4.78 μm. (B) Homogenized model with disc 𝒟_R × {z_o} activated; spr(0.6 s) = 3.21 μm; spr(1.2 s) = 4.58 μm. (C) Activation by the diffusion process (Eq. 24). Homogenized model with activation site at the center of the disc 𝒟_R × {z_o}; spr(0.6 s) = 2.66 μm; spr(1.2 s) = 4.01 μm. Common to these panels is that they exhibit radially symmetric solutions and therefore there is no dependence on the angular variable θ. Both dark current suppression and spread decrease for higher space resolution of the model.

FIGURE 6

Activation by a point source and the diffusion process (Eq. 24). Activation site (point source) at and (A) Plots of (B) Plots of 1 − J_rel(z, 0, t); spr(0, 0.6 s) = 2.86 μm; spr(0, 1.2 s) = 4.17 μm. (C) Plots of values of

FIGURE 7

Activation by a point source and the diffusion process (Eq. 24). Activation site (point source) at R and (A) Plots of (B) Plots of 1 − J_rel(z, 0, t); spr(0, 0.6 s) = 3.10 μm; spr(0, 1.2 s) = 4.37 μm. (C) Plots of

FIGURE 8

Curves “iso-suppression” at time t = 200 ms, for the five models (1) ROS well stirred in the transversal variables and activation, at the level z_o, by Eqs. 23a and 23b. (2) Homogenized model with activated disc at level z_o. Activation mechanism is Eqs. 23a and 23b. (3) Homogenized model with point-mass activation by the mechanism (Eq. 24). The activated point is on the disc 𝒟_R × {z_o}. (3i) Activation at the center of 𝒟_R × {z_o}. (3ii) Activation at on 𝒟_R × {z_o}. (3iii) Activation at the rim ρ = R of 𝒟_R × {z_o}.