Motion parallax is computed in the updating of human spatial memory
- PMID: 12954876
- PMCID: PMC6740481
- DOI: 10.1523/JNEUROSCI.23-22-08135.2003
Motion parallax is computed in the updating of human spatial memory
Abstract
As we move through space, stationary objects around us show motion parallax: their directions relative to us change at different rates, depending on their distance. Does the brain incorporate parallax when it updates its stored representations of space? We had subjects fixate a distant target and then we flashed lights, at different distances, onto the retinal periphery. Subjects translated sideways while keeping their gaze on the distant target, and then they looked to the remembered location of the flash. Their responses corrected almost perfectly for parallax: they turned their eyes farther for nearer targets, in the predicted nonlinear patterns. Computer simulations suggest a neural mechanism in which feedback about self-motion updates remembered locations of objects within an internal map of three-dimensional visual space.
Figures



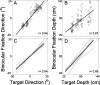


 , with x indicating the vector cross-product). Both signals, computed in eye coordinates, are used to update the retinotopic target map. Updating circuits use local information about target depth and direction (as stored in the target map) to determine how that same representation is remapped during the motion. B, The derivation of the updating equation (Eq. 3). If the eyes are rotating, the target moves in opposite direction relative to the eyes, according to
, with x indicating the vector cross-product). Both signals, computed in eye coordinates, are used to update the retinotopic target map. Updating circuits use local information about target depth and direction (as stored in the target map) to determine how that same representation is remapped during the motion. B, The derivation of the updating equation (Eq. 3). If the eyes are rotating, the target moves in opposite direction relative to the eyes, according to




Similar articles
-
Parallax-sensitive remapping of visual space in occipito-parietal alpha-band activity during whole-body motion.J Neurophysiol. 2015 Mar 1;113(5):1574-84. doi: 10.1152/jn.00477.2014. Epub 2014 Dec 10. J Neurophysiol. 2015. PMID: 25505108 Free PMC article.
-
Spatial updating and the maintenance of visual constancy.Neuroscience. 2008 Oct 28;156(4):801-18. doi: 10.1016/j.neuroscience.2008.07.079. Epub 2008 Aug 22. Neuroscience. 2008. PMID: 18786618 Free PMC article. Review.
-
Gaze-centered updating of remembered visual space during active whole-body translations.J Neurophysiol. 2007 Feb;97(2):1209-20. doi: 10.1152/jn.00882.2006. Epub 2006 Nov 29. J Neurophysiol. 2007. PMID: 17135474
-
Motion parallax from microscopic head movements during visual fixation.Vision Res. 2012 Oct 1;70:7-17. doi: 10.1016/j.visres.2012.07.017. Epub 2012 Aug 8. Vision Res. 2012. PMID: 22902643 Free PMC article.
-
Neural control of 3-D gaze shifts in the primate.Prog Brain Res. 2003;142:109-24. doi: 10.1016/s0079-6123(03)42009-8. Prog Brain Res. 2003. PMID: 12693257 Review.
Cited by
-
Functional organization within a neural network trained to update target representations across 3-D saccades.J Comput Neurosci. 2007 Apr;22(2):191-209. doi: 10.1007/s10827-006-0007-5. J Comput Neurosci. 2007. PMID: 17120151
-
Superior Colliculus Responses to Attended, Unattended, and Remembered Saccade Targets during Smooth Pursuit Eye Movements.Front Syst Neurosci. 2016 Apr 12;10:34. doi: 10.3389/fnsys.2016.00034. eCollection 2016. Front Syst Neurosci. 2016. PMID: 27147987 Free PMC article.
-
Parallax-sensitive remapping of visual space in occipito-parietal alpha-band activity during whole-body motion.J Neurophysiol. 2015 Mar 1;113(5):1574-84. doi: 10.1152/jn.00477.2014. Epub 2014 Dec 10. J Neurophysiol. 2015. PMID: 25505108 Free PMC article.
-
Spatial updating and the maintenance of visual constancy.Neuroscience. 2008 Oct 28;156(4):801-18. doi: 10.1016/j.neuroscience.2008.07.079. Epub 2008 Aug 22. Neuroscience. 2008. PMID: 18786618 Free PMC article. Review.
-
Binocular eye movements evoked by self-induced motion parallax.J Neurosci. 2011 Nov 23;31(47):17069-73. doi: 10.1523/JNEUROSCI.2192-11.2011. J Neurosci. 2011. PMID: 22114276 Free PMC article. Clinical Trial.
References
-
- Amorim MA, Glasauer S, Corpinot K, Berthoz A ( 1997) Updating object's orientation and location during nonvisual navigation: a comparison between two processing modes. Percept Psychophys 59: 404-418. - PubMed
-
- Andersen RA, Essick GK, Siegel RM ( 1985) Encoding of spatial location by posterior parietal neurons. Science 230: 456-458. - PubMed
-
- Andersen RA, Shenoy KV, Snyder LH, Bradley DC, Crowell JA ( 1999) The contributions of vestibular signals to the representations of space in the posterior parietal cortex. Ann NY Acad Sci 871: 282-292. - PubMed
-
- Angelaki DE ( 1998) Three-dimensional organization of otolith-ocular reflexes in rhesus monkeys. III. Responses to translation. J Neurophysiol 80: 680-695. - PubMed
-
- Batista AP, Buneo CA, Snyder LH, Andersen RA ( 1999) Reach plans in eye-centered coordinates. Science 285: 257-260. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Research Materials
