The role of certain Post classes in Boolean network models of genetic networks

Abstract

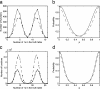
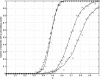
A topic of great interest and debate concerns the source of order and remarkable robustness observed in genetic regulatory networks. The study of the generic properties of Boolean networks has proven to be useful for gaining insight into such phenomena. The main focus, as regards ordered behavior in networks, has been on canalizing functions, internal homogeneity or bias, and network connectivity. Here we examine the role that certain classes of Boolean functions that are closed under composition play in the emergence of order in Boolean networks. The closure property implies that any gene at any number of steps in the future is guaranteed to be governed by a function from the same class. By means of Derrida curves on random Boolean networks and percolation simulations on square lattices, we demonstrate that networks constructed from functions belonging to these classes have a tendency toward ordered behavior. Thus they are not overly sensitive to initial conditions, and damage does not readily spread throughout the network. In addition, the considered classes are significantly larger than the class of canalizing functions as the connectivity increases. The functions in these classes exhibit the same kind of preference toward biased functions as do canalizing functions, meaning that functions from this class are likely to be biased. Finally, functions from this class have a natural way of ensuring robustness against noise and perturbations, thus representing plausible evolutionarily selected candidates for regulatory rules in genetic networks.

Fig. 1.

(a and c) Subplots, with K = 4 and 5, respectively, show histograms of the number of canalizing (solid line) and A² ∪ a² (dashed line) functions versus the number of ones in their truth tables. (b and d) Subplots, with K = 4 and 5, respectively, show the probability that a randomly chosen Boolean function with bias p is a canalizing (solid line) or A² ∪ a² (dashed line) function.

Fig. 2.

A comparison between 4K and ψ(K) for K = 1,..., 7. A logarithmic scale is used. Because ψ(K) grows much faster than 4K, the number of A² functions grows much faster than the number of canalizing functions.

Fig. 3.

Derrida curves corresponding to several classes. (a) Canalizing functions (solid line), the class A² ∪ a² (dashed line), and random Boolean functions (dash-dot line) (K = 4). (b) Post classes A² (solid line), A³ (dashed line), and A⁴ = A^∞ (dash-dot line) (K = 4). (c) Post classes A² for K = 3 (solid line), 4 (dashed line), and 5 (dash-dot line).

Fig. 4.

Percolation results of random networks constructed by using several classes of Boolean functions. The horizontal axis shows the fraction of functions belonging to a given class. The vertical axis shows the fraction of networks that contain a spanning (percolating) cluster of frozen genes. The classes are A² (×), A³ (▿), A⁴ (+), canalizing (○), and A² ∪ a² (▵). The size of the lattice is 50 × 50 (2,500 genes). For each q (51 equally spaced values), 100 networks were constructed for computing the fraction of those containing percolating clusters.