INDOCYANINE GREEN DENSITOMETRY IN FLOWING BLOOD COMPENSATED FOR BACKGROUND DYE
- PMID: 14080764
- PMCID: PMC2997752
- DOI: 10.1152/jappl.1963.18.6.1294
INDOCYANINE GREEN DENSITOMETRY IN FLOWING BLOOD COMPENSATED FOR BACKGROUND DYE
Abstract
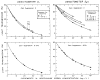
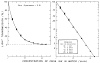
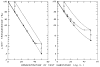
Blood is nonhomogeneous; hence, the relationship between light transmission and increasing concentration of dye in whole blood is never the perfect exponential curve predicted by Beer’s law. Instead, as the concentration of indocyanine green is increased to high levels (40 mg/liter) the light transmission decreases exponentially toward an asymptote at 6–8% transmission for nearly monochromatic densitometers (half-band width: 13–20 mμ), but at 30–40% for densitometers using light of wide-band width. Consequently, following recording of a dilution curve, circulating background dye reduces the change in transmission per unit increase in dye concentration in subsequent curves. This decrease in sensitivity cannot be compensated for by a simple increase in the sensitivity of the densitometer or in the intensity of its light source. Compensation can be attained, however, if increasing densitometer sensitivity is associated with the automatic scale expansion provided when a suppressed zero point is used. At correct zero suppression, the deflection for zero output of the densitometer coincides with the asymptotic transmission value mentioned above.
Figures




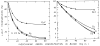





References
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
