Dynamic tension spectroscopy and strength of biomembranes

Abstract

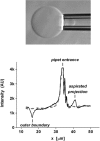
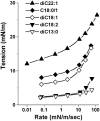
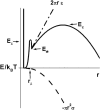
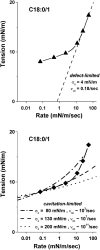
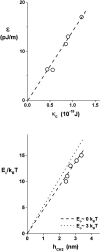
Rupturing fluid membrane vesicles with a steady ramp of micropipette suction produces a distribution of breakage tensions governed by the kinetic process of membrane failure. When plotted as a function of log(tension loading rate), the locations of distribution peaks define a dynamic tension spectrum with distinct regimes that reflect passage of prominent energy barriers along the kinetic pathway. Using tests on five types of giant phosphatidylcholine lipid vesicles over loading rates(tension/time) from 0.01-100 mN/m/s, we show that the kinetic process of membrane breakage can be modeled by a causal sequence of two thermally-activated transitions. At fast loading rates, a steep linear regime appears in each spectrum which implies that membrane failure starts with nucleation of a rare precursor defect. The slope and projected intercept of this regime are set by defect size and frequency of spontaneous formation, respectively. But at slow loading rates, each spectrum crosses over to a shallow-curved regime where rupture tension changes weakly with rate. This regime is predicted by the classical cavitation theory for opening an unstable hole in a two-dimensional film within the lifetime of the defect state. Under slow loading, membrane edge energy and the frequency scale for thermal fluctuations in hole size are the principal factors that govern the level of tension at failure. To critically test the model and obtain the parameters governing the rates of transition under stress, distributions of rupture tension were computed and matched to the measured histograms through solution of the kinetic master (Markov) equations for defect formation and annihilation or evolution to an unstable hole under a ramp of tension. As key predictors of membrane strength, the results for spontaneous frequencies of defect formation and hole edge energies were found to correlate with membrane thicknesses and elastic bending moduli, respectively.

FIGURE 1

(Top) Video microscope image of a 20-μm (C18:0/1) PC bilayer vesicle aspirated into a micropipette. (Bottom) Intensity scans taken along the axis of symmetry before (solid curve) and the next video step 0.01 s after (dotted curve) vesicle rupture.

FIGURE 2

Membrane tension as function of time for two vesicles made from diC18:2 PC; one loaded at slow rate and the other at fast rate up to rupture (noted by asterisks).

FIGURE 3

Comparative histograms of rupture tensions collected at slow (top row) and fast (bottom row) loading rates for vesicles made from (left) diC13:0 PC, (middle) C18:0/1 PC, and (right) diC22:1 PC. Superposed on each distribution is the probability density for failure predicted by the kinetic model for membrane rupture and the parameters listed in Table 1.

FIGURE 4

Dynamic tension spectra defined by the plots of most frequent rupture tension as a function of log(tension loading rate). Superposed are continuous curves predicted by the kinetic model for membrane rupture and the parameters listed in Table 1.

FIGURE 5

Schematic of the energy landscape in hole radius space used to model the kinetic process of membrane rupture. The precursor barrier E_δ at r_δ governs creation of a molecular-scale defect that then either vanishes or passes over the outer cavitation barrier to catastrophic failure. The height E_c of the cavitation barrier above the metastable state at energy E_* is set by hole edge energy, ɛ, and mechanical tension, σ; i.e., E_c − E_* = πɛ²/σ.

FIGURE 6

Demonstration of the initial step in analysis of DTS measurements using the spectrum from tests on C18:0/1 PC vesicles. (Top) A straight line fit to high strengths at fast loading rates represents defect-limited kinetics. The intercept and slope of this line reveal the spontaneous frequency for formation of defects, ν_oδ ∼ 0.18/s, and tension scale for rate exponentiation, σ_δ ∼ 4 mN, as set by defect area (i.e., σ_δ = k_BT/πr_δ²). (Bottom) Three shallow-curved regimes matched to the slowest loading rate result represent cavitation-limited kinetics. As noted on the figure and described in the text, each of these curves depends on a second tension scale, σ_c, which is set by hole edge energy (i.e., σ_c = πɛ²/k_BT), and an attempt frequency, ν_δc, for passage of the cavitation barrier. To fit the data over an extended span in loading rate, the parameter values were restricted to σ_c ≈ 130 mN/m with corresponding rate scale ν_δc ∼ 10⁷/s.

FIGURE 7

(Top) Correlation of hole edge energy from Table 1 to membrane elastic-bending stiffness as measured by micromechanical tests (Rawicz et al., 2000). (Bottom) Correlation of defect barrier energy estimated from the ratios of tension (σ_δ/σ_c) and frequency (ν_δc/ν_o) scales in Table 1 to membrane core-hydrocarbon thickness as derived from x-ray diffraction measurements (Rawicz et al., 2000). Described in the text, defect barrier energy is defined by E_δ/k_BT ≈ Log_e(σ_δ/σ_c) + Log_e(ν_δc / ν_o). The open circles are values of ν_δc in Table 1 based on a lower bound of E_o ∼ 0 k_BT. At E_o ∼ 3 k_BT, values of ν_δc are increased 10-fold and barrier energies shift upward correspondingly.