Measuring spike coding in the rat supraoptic nucleus
- PMID: 14608010
- PMCID: PMC1664829
- DOI: 10.1113/jphysiol.2003.053264
Measuring spike coding in the rat supraoptic nucleus
Abstract
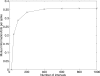
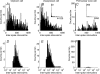
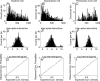
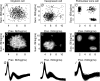
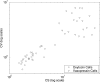
Measuring spike coding objectively is essential to establish whether activity recorded under one set of conditions is truly different from that recorded under another set of conditions. However, there is no generally accepted method for making such comparisons. Measuring firing frequency alone only partially reflects spike patterning. In this paper, novel quantities based on the logarithmic interspike intervals are proposed as useful measures of spontaneous activity. We illustrate the methods by comparing extracellular recordings from magnocellular cells of the rat supraoptic nucleus in vivo and in vitro and between oxytocin and vasopressin cells in vivo. A bimodal Gaussian function fitted to the log interspike interval histogram accurately described the distribution profile for very different types of activity. We introduce the entropy of the log interval distribution as a novel quantity that measures the capacity of a cell to encode information other than a constant instantaneous frequency. Unlike existing entropy measures that are based on spike counts, it quantifies the variability in the interval distribution. In addition, the mutual information between adjacent log intervals is proposed as an objective measure of patterned activity. For cells recorded in vivo and in vitro, there was no significant difference in mean spike frequencies but there were differences in the log interval entropy (t = -4.97, P < 0.001) and the mutual information (z = -2.64, P < 0.01). The differences may result from the disruption of connections in the slice preparation. When a comparison was made between the spike activity of oxytocin and vasopressin cells recorded in vivo, there was a difference in mutual information (z = 5.15, P < 0.001) but not in mean spike frequency. Both comparisons highlight the potential limitations of using mean spike frequency alone as a measure of spike coding. We propose that our novel parameters based on interval analysis constitute informative measures of spontaneous activity under different physiological conditions.
Figures

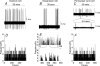



References
-
- Aitchison J, Brown J. The Lognormal Distribution. Cambridge: Cambridge University Press; 1963.
-
- Andrew R, Dudek F. Analysis of intracellularly recorded phasic bursting by mammalian neuroendocrine cells. J Neurophysiol. 1984;51:552–566. - PubMed
-
- Armstrong W, Stern J. Electrophysiological and morphological characteristics of neurons in perinuclear zone of supraoptic nucleus. J Neurophysiol. 1997;78:2427–2437. - PubMed
-
- Bhumbra G, Wakerley J, Dyball R. A novel approach to reveal spike coding in rat oxytocin cells. J Physiol. 2003;547:C78. P.
-
- Bialek W, Rieke F, de Ruyter Van Steveninck R, Warland D. Reading a neural code. Science. 1991;252:1854–1857. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

