A statistical sampling algorithm for RNA secondary structure prediction
- PMID: 14654704
- PMCID: PMC297010
- DOI: 10.1093/nar/gkg938
A statistical sampling algorithm for RNA secondary structure prediction
Abstract
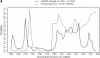
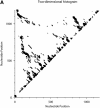
An RNA molecule, particularly a long-chain mRNA, may exist as a population of structures. Further more, multiple structures have been demonstrated to play important functional roles. Thus, a representation of the ensemble of probable structures is of interest. We present a statistical algorithm to sample rigorously and exactly from the Boltzmann ensemble of secondary structures. The forward step of the algorithm computes the equilibrium partition functions of RNA secondary structures with recent thermodynamic parameters. Using conditional probabilities computed with the partition functions in a recursive sampling process, the backward step of the algorithm quickly generates a statistically representative sample of structures. With cubic run time for the forward step, quadratic run time in the worst case for the sampling step, and quadratic storage, the algorithm is efficient for broad applicability. We demonstrate that, by classifying sampled structures, the algorithm enables a statistical delineation and representation of the Boltzmann ensemble. Applications of the algorithm show that alternative biological structures are revealed through sampling. Statistical sampling provides a means to estimate the probability of any structural motif, with or without constraints. For example, the algorithm enables probability profiling of single-stranded regions in RNA secondary structure. Probability profiling for specific loop types is also illustrated. By overlaying probability profiles, a mutual accessibility plot can be displayed for predicting RNA:RNA interactions. Boltzmann probability-weighted density of states and free energy distributions of sampled structures can be readily computed. We show that a sample of moderate size from the ensemble of an enormous number of possible structures is sufficient to guarantee statistical reproducibility in the estimates of typical sampling statistics. Our applications suggest that the sampling algorithm may be well suited to prediction of mRNA structure and target accessibility. The algorithm is applicable to the rational design of small interfering RNAs (siRNAs), antisense oligonucleotides, and trans-cleaving ribozymes in gene knock-down studies.
Figures






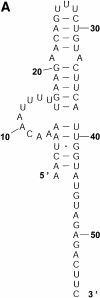
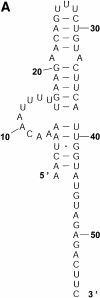
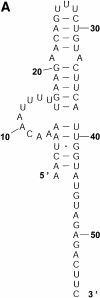



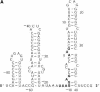
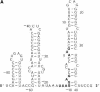















References
-
- More P.B. and Steitz,T.A. (2003). The structural basis of large ribosomal subunit function. Annu. Rev. Biochem., 72, 813–850. - PubMed
-
- McCaskill J.S. (1990) The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers, 29, 1105–1119. - PubMed
-
- Bonhoeffer S., McCaskill,J.S., Stadler,P.F. and Schuster,P. (1993) RNA multi-structure landscapes. A study based on temperature dependent partition functions. Eur. Biophys. J., 22, 13–24. - PubMed
-
- Christoffersen R.E., McSwiggen,J.A. and Konings,D. (1994) Application of computational technologies to ribozyme biotechnology products. J. Mol. Struct. (Theochem.), 311, 273–284.

