Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Jan 30;23(2):199-210.
doi: 10.1002/sim.1709.

Incidence and mortality of Alzheimer's disease or dementia using an illness-death model

D Commenges  1 , P Joly, L Letenneur, J F Dartigues
Affiliations
Free PMC article

Incidence and mortality of Alzheimer's disease or dementia using an illness-death model

D Commenges et al. Stat Med. .
Free PMC article

Abstract

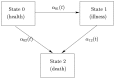
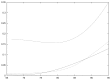
We present an illness-death model for studying the incidence and the prevalence of Alzheimer's disease or dementia. We argue that the illness-death model is better than a survival model for this purpose. In this model the best choice for the basic time-scale is age. Then we present extensions of this model for incorporating covariates and taking account of a possible effect of calendar time. Calendar time is introduced via a proportional intensity model. We give the likelihood for a mixed discrete-continuous observation pattern from this model: clinical status is observed at discrete visit-times while the date of death is observed exactly or right-censored. The penalized likelihood approach allows to non-parametrically estimate the transition intensities. Application on the data of the Paquid study allows to produce estimates of the age-specific incidence of dementia together with mortality rates of both demented and non-demented subjects. Then the effect of calendar time and educational level are studied. Low educational level increases the risk of dementia. The risk of dementia increases with calendar time while the mortality of demented subjects decreases. The most likely explanation of this result seems to be in a shift in the diagnosis of dementia towards earlier stages of the disease prompted by a change in the perception of dementia and the arrival of new drugs.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Graphical representation of an illness-death model.
Figure 2
Figure 2
Age-specific incidence of dementia and mortality rates for women. Upper dotted line: mortality rate for demented; lower dotted line: mortality rate for non-demented; continuous line: incidence of dementia.
Figure 3
Figure 3
Age-specific incidence of dementia and mortality rates for men. Upper dotted line: mortality rate for demented; lower dotted line: mortality rate for non-demented; continuous line: incidence of dementia.
Figure 4
Figure 4
Age-specific incidence of dementia and mortality rates for non-demented for the global sample based on 8-year and 10-year of follow–up. The two mortality rates are the upper curves and are indistinguishable; the lowest (dotted) line is the age-specific incidence based on the 8-year follow-up; the curve just above (continuous) is the age-specific incidence based on the 10-year follow-up.
See this image and copyright information in PMC

References

    1. Peto R. Experimental survival curves for interval-censored data. Applied Statistics. 1973;22:86–91.
    1. Turnbull BW. The empirical distribution function with arbitrarily grouped, censored and truncated data. Journal of the Royal Statistical Society, Series B. 1976;38:290–5.
    1. Finkelstein D. A proportional hazards model for interval-censored failure time data. Biometrics. 1986;42:845–854. - PubMed
    1. Alioum A, Commenges D. A proportional hazards model for arbitrarily censored and truncated data. Biometrics. 1996;52:95–107. - PubMed
    1. Joly P, Commenges D, Letenneur L. A penalized likelihood approach for arbitrarily censored and truncated data: application to age-specific incidence of dementia. Biometrics. 1998;54:203–212. - PubMed