The simultaneous evolution of author and paper networks

Abstract

There has been a long history of research into the structure and evolution of mankind's scientific endeavor. However, recent progress in applying the tools of science to understand science itself has been unprecedented because only recently has there been access to high-volume and high-quality data sets of scientific output (e.g., publications, patents, grants) and computers and algorithms capable of handling this enormous stream of data. This article reviews major work on models that aim to capture and recreate the structure and dynamics of scientific evolution. We then introduce a general process model that simultaneously grows coauthor and paper citation networks. The statistical and dynamic properties of the networks generated by this model are validated against a 20-year data set of articles published in PNAS. Systematic deviations from a power law distribution of citations to papers are well fit by a model that incorporates a partitioning of authors and papers into topics, a bias for authors to cite recent papers, and a tendency for authors to cite papers cited by papers that they have read. In this TARL model (for topics, aging, and recursive linking), the number of topics is linearly related to the clustering coefficient of the simulated paper citation network.

Fig. 1.

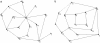
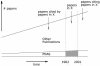
Process model in pseudo code. If no topics are considered then the number of topics is one, i.e., all papers and authors have the same topic. If no coauthors are considered then each paper has exactly one author. If the reference path length is 0 then no references are considered for citation. If no aging function is given then all papers have the same probability of getting selected.

Fig. 2.

Author-paper network generated by using the model with topics only (a) and coauthors only (b). The model was started with five topics, authors, and papers and run for 2 years. In each year, each author produces one paper, which cites two earlier papers. No authors were added or deactivated. The resulting networks has five authors (labeled a1-a5, blue circles) and 15 or 9 papers (labeled 0, 2, 3..., red triangles). Papers are linked via red directed provided input to links. Authors are connected by blue coauthorships links. Light green indicates directed links denoting the flow of information from papers to authors and from authors to new papers via consumed and produced relations.

Fig. 3.

Paper network without aging (a) and with aging (b). Without aging, older papers are more likely to provide input to younger papers; i.e., they are attracting most of the citation links. For example, in a, paper no. 0 generated at initialization time and paper no. 5 generated in year 1 provide input to four and six papers, respectively.

Fig. 4.

Coverage of the PNAS data set in terms of time span, total papers, and complete authors' work.

Fig. 5.

Total number of actual and simulated papers (#p) and authors (#a) (a) and received citations (#c_win) (b).

Fig. 6.

Cluster coefficient as a function of the aging function (a) and the reference path length (b).