Modeling extracellular field potentials and the frequency-filtering properties of extracellular space
- PMID: 14990509
- PMCID: PMC1304017
- DOI: 10.1016/S0006-3495(04)74250-2
Modeling extracellular field potentials and the frequency-filtering properties of extracellular space
Abstract
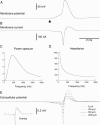
Extracellular local field potentials are usually modeled as arising from a set of current sources embedded in a homogeneous extracellular medium. Although this formalism can successfully model several properties of extracellular local field potentials, it does not account for their frequency-dependent attenuation with distance, a property essential to correctly model extracellular spikes. Here we derive expressions for the extracellular potential that include this frequency-dependent attenuation. We first show that, if the extracellular conductivity is nonhomogeneous, there is induction of nonhomogeneous charge densities that may result in a low-pass filter. We next derive a simplified model consisting of a punctual (or spherical) current source with spherically symmetric conductivity/permittivity gradients around the source. We analyze the effect of different radial profiles of conductivity and permittivity on the frequency-filtering behavior of this model. We show that this simple model generally displays low-pass filtering behavior, in which fast electrical events (such as Na(+)-mediated action potentials) attenuate very steeply with distance, whereas slower (K(+)-mediated) events propagate over larger distances in extracellular space, in qualitative agreement with experimental observations. This simple model can be used to obtain frequency-dependent extracellular field potentials without taking into account explicitly the complex folding of extracellular space.
Figures




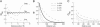

References
-
- Amzica, F. 2002. In vivo electrophysiological evidences for cortical neuron-glia interactions during slow (<1 Hz) and paroxysmal sleep oscillations. J. Physiol. (Paris). 96:209–219. - PubMed
-
- Basser, P. J., and B. J. Roth. 2000. New currents in electrical stimulation of excitable tissues. Annu. Rev. Biomed. Eng. 2:377–397. - PubMed
-
- Braitenberg, V., and A. Schüz. 1998. Cortex: statistics and geometry of neuronal connectivity, 2nd ed. Springer-Verlag, Berlin, Germany.
-
- Bremer, F. 1938. L'activité électrique de l'écorce cérébrale. Actualités Scientifiques et Industrielles. 658:3–46.
-
- Bremer, F. 1949. Considérations sur l'origine et la nature des “ondes” cérébrales. Electroencephalogr. Clin. Neurophysiol. 1:177–193. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases

