Analytic models for mechanotransduction: gating a mechanosensitive channel

Abstract

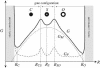
Analytic estimates for the forces and free energy generated by bilayer deformation reveal a compelling and intuitive model for MscL channel gating analogous to the nucleation of a second phase. We argue that the competition between hydrophobic mismatch and tension results in a surprisingly rich story that can provide both a quantitative comparison with measurements of opening tension for MscL when reconstituted in bilayers of different thickness, and qualitative insights into the function of the MscL channel and other transmembrane proteins.

Fig. 1.

The bilayer–inclusion model. The geometry of the inclusion is described by three parameters: R, the radius; W, the hydrophobic thickness; and H′, the radial midplane slope. The hydrophobic mismatch, 2U, is the difference between the hydrophobic protein thickness, W, and the bilayer equilibrium thickness, 2a. We assume the surfaces of the bilayer are locally normal to the interface of the inclusion, as depicted, implying that the midplane slope is related to the interface angle: H′ = tan θ.

Fig. 2.

The bilayer deformation energy landscape. The bilayer deformation energy is plotted as a function of the radius for different values of applied tension. The solid curves represent the bilayer deformation energy with a positive line tension, f, for various different tensions (0 < α₁ < α₂ < α₃ < α₄). The competition between interface energy and applied tension naturally gives rise to a bistable potential when the radial domain is limited by steric constraints. The gray regions represent radii inaccessible to the channel because of steric constraints. These constraints are briefly motivated in The Energy Landscape of the Bilayer. If the line tension is negative, depicted by the dotted curve, the potential is never bistable.

Fig. 3.

The total free energy. The total free energy, G, of the protein and bilayer are plotted schematically as a function of channel radius. The bilayer deformation energy, , is represented by the dotted curve. A protein conformation energy is represented schematically by the dashed curve. Their sum gives the total free energy G. The protein energy has been chosen to contain a single substate, S. A conformational energy barrier is shown that corresponds to changing the gate conformation of the channel. These transitions occur at R_CS and R_SO. G_P also contains steep barriers corresponding to steric constraints. The radii of the conductance states are defined by the free-energy minima of G.

Fig. 4.

The free-energy difference between open and closed states vs. lipid acyl chain length. The experimental data of Perozo et al. (5) for the free-energy difference between the open and closed states at zero tension, ΔG₀, is plotted with black circles and error bars. The solid curve represents the theoretical values for the bilayer deformation energy generated by a simple thickness-deformation model at zero tension, . The dotted curve represents the translated for an engineered MscL channel with a hydrophobic thickness matching a PC14 bilayer.