Assessing the probability that a positive report is false: an approach for molecular epidemiology studies

Abstract

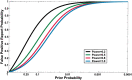
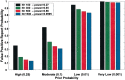
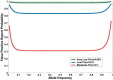
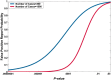
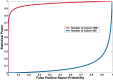
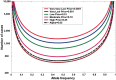
Too many reports of associations between genetic variants and common cancer sites and other complex diseases are false positives. A major reason for this unfortunate situation is the strategy of declaring statistical significance based on a P value alone, particularly, any P value below.05. The false positive report probability (FPRP), the probability of no true association between a genetic variant and disease given a statistically significant finding, depends not only on the observed P value but also on both the prior probability that the association between the genetic variant and the disease is real and the statistical power of the test. In this commentary, we show how to assess the FPRP and how to use it to decide whether a finding is deserving of attention or "noteworthy." We show how this approach can lead to improvements in the design, analysis, and interpretation of molecular epidemiology studies. Our proposal can help investigators, editors, and readers of research articles to protect themselves from overinterpreting statistically significant findings that are not likely to signify a true association. An FPRP-based criterion for deciding whether to call a finding noteworthy formalizes the process already used informally by investigators--that is, tempering enthusiasm for remarkable study findings with considerations of plausibility.

Fig. 1.

Effect of changes in prior probability and statistical power on false positive report probability (FPRP) when the α level is .05. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. A low FPRP is achievable only for high prior probabilities. Moreover, statistical power has an important impact on FPRP, except for particularly high and low prior probabilities. For example, for a prior probability of 0.1, the FPRPs are 0.69, 0.47, 0.36, and 0.31 for statistical powers of 0.2, 0.5, 0.8, and 1.

Fig. 2.

Effect of sample size on false positive report probability (FPRP). In this figure, allele frequency q = .3, α = .05, and statistical power is for detecting an odds ratio of 1.5. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. Prior probability and N (numbers of case patients and control subjects) have a large effect on the FPRP. FPRP remains very high with a low prior probability (.001). Increasing the sample size beyond N = 1500 case patients and control subjects will have only a marginal effect on FPRP because statistical power is already close to 1.

Fig. 3.

False positive report probability (FPRP) as function of allele frequency (q) of a high-risk allele for three prior probabilities. In this figure, α = .05, N = 1500 case patients and control subjects, and statistical power is calculated for detecting an odds ratio of 1.5. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. Allele frequency affects FPRP through its effect on statistical power.

Fig. 4.

Effect of sample size on the relation between the P value and false-positive report probability (FPRP). FPRP is shown as a function of the P value for two sample sizes, N = 300 and N = 1500, when the prior probability is 0.001, the allele frequency (q) is 0.3, and statistical power is shown to detect an odds ratio of 1.5. The FPRP value can be very different even when the P value and prior probability are the same because of differences in statistical power.

Fig. 5.

Effect of decreasing the false positive report probability (FPRP) required to declare a finding noteworthy on statistical power. Statistical power is shown to detect an odds ratio of 1.5, with a prior probability of 0.001 and an allele frequency (q) of .3 for 300 and for 1500 case patients and control subjects. Note the trade-off between increased statistical power and a lowered FPRP for a fixed sample size and the potential increase in statistical power with the same FPRP but larger sample size.

Fig. 6.

Sample size needed to achieve a false positive report probability (FPRP) value of 0.2 with various prior probabilities or with an α level of .05 (black broken line) for traditional sample size (N) calculations. Sample size is shown for various allele frequencies (q), with statistical power of 0.8 to detect an odds ratio of 1.5.