Enriching for direct regulatory targets in perturbed gene-expression profiles
- PMID: 15059262
- PMCID: PMC395788
- DOI: 10.1186/gb-2004-5-4-r29
Enriching for direct regulatory targets in perturbed gene-expression profiles
Abstract
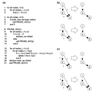
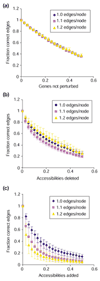
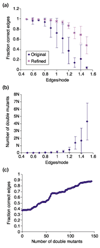
Here we build on a previously proposed algorithm to infer direct regulatory relationships using gene-expression profiles from cells in which individual genes are deleted or overexpressed. The updated algorithm can process networks containing feedback loops, incorporate positive and negative regulatory relationships during network reconstruction, and utilize data from double mutants to resolve ambiguous regulatory relationships. When applied to experimental data the reconstruction procedure preferentially retains direct transcription factor-target relationships.
Figures
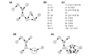

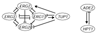
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

