Receiver operating characteristic (ROC) curve: practical review for radiologists

Abstract

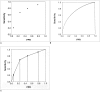
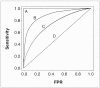
The receiver operating characteristic (ROC) curve, which is defined as a plot of test sensitivity as they coordinate versus its 1-specificity or false positive rate (FPR) as the x coordinate, is an effective method of evaluating the performance of diagnostic tests. The purpose of this article is to provide a nonmathematical introduction to ROC analysis. Important concepts involved in the correct use and interpretation of this analysis, such as smooth and empirical ROC curves, parametric and nonparametric methods, the area under the ROC curve and its 95% confidence interval, the sensitivity at a particular FPR, and the use of a partial area under the ROC curve are discussed. Various considerations concerning the collection of data in radiological ROC studies are briefly discussed. An introduction to the software frequently used for performing ROC analyses is also presented.

Fig. 1

ROC curves from a plain chest radiography study of 70 patients with solitary pulmonary nodules (Table 3). A. A plot of test sensitivity (y coordinate) versus its false positive rate (x coordinate) obtained at each cutoff level. B. The fitted or smooth ROC curve that is estimated with the assumption of binormal distribution. The parametric estimate of the area under the smooth ROC curve and its 95% confidence interval are 0.734 and 0.602 ~ 0.839, respectively. C. The empirical ROC curve. The discrete points on the empirical ROC curve are marked with dots. The nonparametric estimate of the area under the empirical ROC curve and its 95% confidence interval are 0.728 and 0.608 ~ 0.827, respectively. The nonparametric estimate of the area under the empirical ROC curve is the summation of the areas of the trapezoids formed by connecting the points on the ROC curve.

Fig. 2

Four ROC curves with different values of the area under the ROC curve. A perfect test (A) has an area under the ROC curve of 1. The chance diagonal (D, the line segment from 0, 0 to 1, 1) has an area under the ROC curve of 0.5. ROC curves of tests with some ability to distinguish between those subjects with and those without a disease (B, C) lie between these two extremes. Test B with the higher area under the ROC curve has a better overall diagnostic performance than test C.

Fig. 3

Two ROC curves (A and B) with equal area under the ROC curve. However, these two ROC curves are not identical. In the high false positive rate range (or high sensitivity range) test B is better than test A, whereas in the low false positive rate range (or low sensitivity range) test A is better than test B.

Fig. 4

Schematic illustration of a comparison between the sensitivities of two ROC curves (A and B) at a particular false positive rate and comparison between two partial ROC areas. For this example, the false positive rate and partial range of false positive rate (e₁ - e₂) are arbitrarily chosen as 0.7 and 0.6 ~ 0.8, respectively.