Response of complex networks to stimuli

Abstract

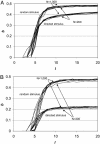
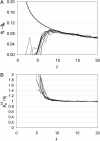
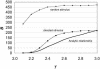
We consider the response of complex systems to stimuli and argue for the importance of both sensitivity, the possibility of large response to small stimuli, and robustness, the possibility of small response to large stimuli. Using a dynamic attractor network model for switching of patterns of behavior, we show that the scale-free topologies often found in nature enable more sensitive response to specific changes than do random networks. This property may be essential in networks where appropriate response to environmental change is critical and may, in such systems, be more important than features, such as connectivity, often used to characterize network topologies. Phenomenologically observed exponents for functional scale-free networks fall in a range corresponding to the onset of particularly high sensitivities, while still retaining robustness.

Fig. 1.

Histograms of the number of changed nodes (basin of attraction, B) needed to change the state of a network with two randomly selected functional states in a network of 1,000 nodes; 1,000 simulations were performed for each histogram. With directed stimuli, random selection was made between nodes of equal connectivity.

Fig. 2.

Size of basin of attraction (fraction of total nodes, b) as a function of the average number of links per node, l, for random and directed stimuli for the two model networks: exponential (A) and scale-free (B). Each family of curves includes simulations from n = 200 to 1,000 in increments of 100, showing the weak variation with network size.

Fig. 3.

Comparisons of simulations with analytic results. Different curves are for different network sizes, as in Fig. 2. (A) Plot of the difference b_r – b_m for exponential networks as a function of the number of links per node. The upper bound obtained in the text is shown as a thick line. (B) Plot of the ratio b^1/2 m /b_r for scale-free networks as a function of the number of links per node.

Fig. 4.

Size B of the basin of attraction for random and directed stimuli for scale-free networks as a function of γ for n = 1,000 node networks and l = 10. The line representing the analytic relationship is Eq. 10.