Biochemical Network Stochastic Simulator (BioNetS): software for stochastic modeling of biochemical networks
- PMID: 15113411
- PMCID: PMC408466
- DOI: 10.1186/1471-2105-5-24
Biochemical Network Stochastic Simulator (BioNetS): software for stochastic modeling of biochemical networks
Abstract
Background: Intrinsic fluctuations due to the stochastic nature of biochemical reactions can have large effects on the response of biochemical networks. This is particularly true for pathways that involve transcriptional regulation, where generally there are two copies of each gene and the number of messenger RNA (mRNA) molecules can be small. Therefore, there is a need for computational tools for developing and investigating stochastic models of biochemical networks.
Results: We have developed the software package Biochemical Network Stochastic Simulator (BioNetS) for efficiently and accurately simulating stochastic models of biochemical networks. BioNetS has a graphical user interface that allows models to be entered in a straightforward manner, and allows the user to specify the type of random variable (discrete or continuous) for each chemical species in the network. The discrete variables are simulated using an efficient implementation of the Gillespie algorithm. For the continuous random variables, BioNetS constructs and numerically solves the appropriate chemical Langevin equations. The software package has been developed to scale efficiently with network size, thereby allowing large systems to be studied. BioNetS runs as a BioSpice agent and can be downloaded from http://www.biospice.org. BioNetS also can be run as a stand alone package. All the required files are accessible from http://x.amath.unc.edu/BioNetS.
Conclusions: We have developed BioNetS to be a reliable tool for studying the stochastic dynamics of large biochemical networks. Important features of BioNetS are its ability to handle hybrid models that consist of both continuous and discrete random variables and its ability to model cell growth and division. We have verified the accuracy and efficiency of the numerical methods by considering several test systems.
Figures


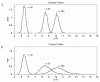
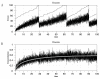

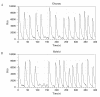

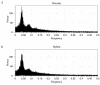

References
-
- Glass L, Kauffman S. The logical analysis of continuous, nonlinear biochemical control networks. J Theor Biol. 1973;39:103–129. - PubMed
-
- Kauffman S. The large-scale structure and dynamics of gene control circuits: An ensemble approach. J Theor Biol. 1974;44:167–190. - PubMed
-
- Savageau M. Comparison of classical and autogenous systems of regulation in inducible operons. Nature. 1974;252:546–549. - PubMed
-
- Glass L. Classification of biological networks by their qualitative dynamics. J Theor Biol. 1975;54:85–107. - PubMed
-
- Tyson J, Othmer H. The dynamics of feedback control circuits in biochemical pathways. Progr Theor Biol. 1978;5:1–60.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

