Geometry and symmetry presculpt the free-energy landscape of proteins

Abstract

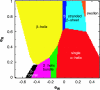
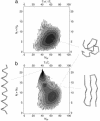
We present a simple physical model that demonstrates that the native-state folds of proteins can emerge on the basis of considerations of geometry and symmetry. We show that the inherent anisotropy of a chain molecule, the geometrical and energetic constraints placed by the hydrogen bonds and sterics, and hydrophobicity are sufficient to yield a free-energy landscape with broad minima even for a homopolymer. These minima correspond to marginally compact structures comprising the menu of folds that proteins choose from to house their native states in. Our results provide a general framework for understanding the common characteristics of globular proteins.

Fig. 1.

Sketch of the local coordinate system. For each C_α atom i (except the first and the last one), the axes of a right-handed local coordinate system are defined as follows. The tangent vector t̂_i is parallel to the segment joining i – 1 with i + i. The normal vector n̂_i joins i to the center of the circle passing through i – 1, i, and i + 1, and it is perpendicular to t̂_i. t̂_iand n̂_i along with the three contiguous C_α atoms lie in a plane shown in the figure. The binormal vector b̂_i is perpendicular to this plane. The vectors t̂_i, n̂_i, and b̂_i are normalized to unit length.

Fig. 2.

Sketch of a portion of a protein chain. (a) The black spheres represent the C_α atoms of the amino acids. The local radius of curvature r is defined as the radius of the circle passing through three consecutive atoms and is constrained to lie between 2.5 Å and 7.9 Å (r_max). A penalty e_R is imposed when 2.5 ≤ r ≤ 3.2 (see b). The hydrophobic interaction, e_W, is operative when two atoms separated by more than two along the sequence are within 7.5 Å of each other (see c). Note that two nonadjacent atoms cannot be closer than 4 Å. A flexible tube is characterized by the constraint that none of the three-body radii is less than the tube thickness, chosen here to be 2.5 Å (see b and d).

Fig. 3.

Phase diagram of ground state conformations. The ground state conformations were obtained by using Monte-Carlo simulations of chains of 24 C_α atoms. e_R and e_W denote the local radius of curvature energy penalty and the solvent-mediated interaction energy, respectively. Over 600 distinct local minima were obtained in different parts of parameter space, starting from a random conformation and successively distorting the chain with pivot and crankshaft moves commonly used in stochastic chain dynamics (43). A Metropolis Monte-Carlo procedure is used with a thermal weight exp(–E/T), where E is the energy of the conformation and the temperature T is set initially at a high value and then decreased gradually to zero. In the orange phase, the ground state is a two-stranded β-hairpin. Two distinct topologies of a three-stranded β-sheet (dark and light blue phases) are found corresponding to conformations shown in conformations i and j in Fig. 4, respectively. The helix bundle shown in conformation b in Fig. 4 is the ground state in the green phase whereas the ground state conformation in the magenta phase has a slightly different arrangement of helices. The white region in the left of the phase diagram has large attractive values of e_W, and the ground state conformations are compact globular structures with a crystalline order induced by hard sphere packing considerations (44) and not by hydrogen bonding (conformation l in Fig. 4).

Fig. 4.

molscript representation of the most common structures obtained in our simulations. Helices and strands are assigned when local or nonlocal hydrogen bonds are formed according to the described rules. Conformations a, b, h, i, j, and k are the stable ground states in different parts of the parameter space shown in Fig. 3. Conformations c, d, e, f, and g are competitive local minima. Conformation l is that of a generic compact polymer chain, obtained by switching off hydrogen bonds, the tube constraint, and curvature energy penalty, and is obtained on maximizing the total number of hydrophobic contacts.

Fig. 5.

Contour plots of the effective free energy at high temperature (T = 0.22) and at the folding transition temperature T_f = 0.2. The effective free energy, defined as F(N_l + N_nl,N_W) =–lnP(N_l + N_nl,N_W), is obtained as a function of the total number of hydrogen bonds N_l + N_nl and the total number of hydrophobic contacts N_W from the histogram P(N_l + N_nl,N_W) collected in equilibrium Monte-Carlo simulations at constant temperature. The spacing between consecutive levels in each contour plot is 1 and corresponds to a free energy difference of , where is the temperature in physical units. The darker the color, the lower the free-energy value. There is just one free-energy minimum corresponding to the denatured state at a temperature higher than the folding transition temperature (a) whereas one can discern the existence of three distinct minima at the folding transition temperature (b). Typical conformations from each of the minima are shown in the figure.