Statics and dynamics of malaria infection in Anopheles mosquitoes
- PMID: 15180900
- PMCID: PMC449722
- DOI: 10.1186/1475-2875-3-13
Statics and dynamics of malaria infection in Anopheles mosquitoes
Abstract
The classic formulae in malaria epidemiology are reviewed that relate entomological parameters to malaria transmission, including mosquito survivorship and age-at-infection, the stability index (S), the human blood index (HBI), proportion of infected mosquitoes, the sporozoite rate, the entomological inoculation rate (EIR), vectorial capacity (C) and the basic reproductive number (R0). The synthesis emphasizes the relationships among classic formulae and reformulates a simple dynamic model for the proportion of infected humans. The classic formulae are related to formulae from cyclical feeding models, and some inconsistencies are noted. The classic formulae are used to to illustrate how malaria control reduces malaria transmission and show that increased mosquito mortality has an effect even larger than was proposed by Macdonald in the 1950's.
Figures

 , is plotted to illustrate the shape of the curve, assuming a human infectious period of 100 days (r = 0.01) and transmission efficiency to humans of 50% (b = 0.5). At this rate, 50% of the human population is infectious with a yearly EIR of 7.3 infectious bites. The relationship between R0 and the proportion of infectious humans,
, is plotted to illustrate the shape of the curve, assuming a human infectious period of 100 days (r = 0.01) and transmission efficiency to humans of 50% (b = 0.5). At this rate, 50% of the human population is infectious with a yearly EIR of 7.3 infectious bites. The relationship between R0 and the proportion of infectious humans,  , is also plotted assuming a human feeding rate of 3 human bites every ten days (a = 0.3), a transmission efficiency to mosquitoes of 50% (c = 0.5), and an average mosquito lifespan of about 10 days (g = 0.1). Note that
, is also plotted assuming a human feeding rate of 3 human bites every ten days (a = 0.3), a transmission efficiency to mosquitoes of 50% (c = 0.5), and an average mosquito lifespan of about 10 days (g = 0.1). Note that  = 0 unless R0 > 1.
= 0 unless R0 > 1.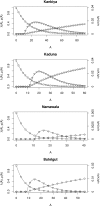

References
-
- Ross R. The prevention of malaria. London: John Murray; 1911.
-
- Macdonald G. The Epidemiology and Control of Malaria. London: Oxford University Press; 1957.
-
- Anderson RM, May RM. Infectious Diseases of Humans. Oxford: Oxford University Press; 1991.
-
- Bailey NTJ. The Biomathematics of Malaria. Oxford University Press; 1982.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

