Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Jun;86(6):3510-8.
doi: 10.1529/biophysj.103.038679.

How to impose microscopic reversibility in complex reaction mechanisms

David Colquhoun  1 , Kathryn A Dowsland, Marco Beato, Andrew J R Plested
Affiliations

How to impose microscopic reversibility in complex reaction mechanisms

David Colquhoun et al. Biophys J. 2004 Jun.

Abstract

Most, but not all, ion channels appear to obey the law of microscopic reversibility (or detailed balance). During the fitting of reaction mechanisms it is therefore often required that cycles in the mechanism should obey microscopic reversibility at all times. In complex reaction mechanisms, especially those that contain cubic arrangements of states, it may not be obvious how to achieve this. Three general methods for imposing microscopic reversibility are described. The first method works by setting the 'obvious' four-state cycles in the correct order. The second method, based on the idea of a spanning tree, works by finding independent cycles (which will often have more than four states) such that the order in which they are set does not matter. The third method uses linear algebra to solve for constrained rates.

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
A four-state cyclic reaction mechanism. The names of the states in this example are intended to indicate that R is a receptor with two different binding sites; either (states 2 and 4) may become occupied before both are occupied (state 1). The labels on the arrows indicate the transition rates and the corresponding equilibrium constants are shown as K1 = k12/k21, K2 = k23/k32, K3 = k43/k34, K4 = k14/k41.
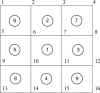
FIGURE 2
FIGURE 2
Representation of a two-dimensional reaction scheme with 16 states (one at each vertex). It contains nine four-membered cycles (numbered 1–9 in the diagram).
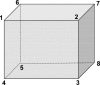
FIGURE 3
FIGURE 3
A reaction mechanism with eight states (vertices) in a cubic arrangement.
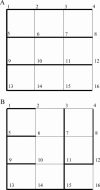
FIGURE 4
FIGURE 4
The 16-state mechanism in Fig. 2, with two examples of the many possible spanning trees shown, as thick lines.
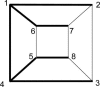
FIGURE 5
FIGURE 5
The cubic mechanism in Fig. 3 is shown projected in two dimensions, with thick lines indicating one of the many possible spanning trees.
See this image and copyright information in PMC

Comment in

References

    1. Colquhoun, D. 1998. Binding, gating, affinity and efficacy. The interpretation of structure- activity relationships for agonists and of the effects of mutating receptors. Br. J. Pharmacol. 125:923–948. - PMC - PubMed
    1. Colquhoun, D., C. J. Hatton, and A. G. Hawkes. 2003. The quality of maximum likelihood estimates of ion channel rate constants. J. Physiol. (Lond.). 547:699–728. - PMC - PubMed
    1. Colquhoun, D., and A. G. Hawkes. 1982. On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Philos. T. Roy. Soc. B. 300:1–59. - PubMed
    1. Colquhoun, D., and A. G. Hawkes. 1987. A note on correlations in single ion channel records. Proc. R. Soc. Lond. B. Biol. Sci. 230:15–52. - PubMed
    1. Colquhoun, D., and A. G. Hawkes. 1995. The principles of the stochastic interpretation of ion channel mechanisms. In Single Channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York. 397–482.

LinkOut - more resources