Using a hybrid neural system to reveal regulation of neuronal network activity by an intrinsic current

Abstract

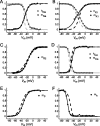
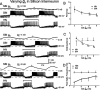
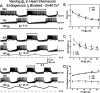
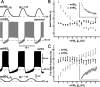
The generation of rhythmic patterns by neuronal networks is a complex phenomenon, relying on the interaction of numerous intrinsic and synaptic currents, as well as modulatory agents. To investigate the functional contribution of an individual ionic current to rhythmic pattern generation in a network, we constructed a hybrid system composed of a silicon model neuron and a heart interneuron from the heartbeat timing network of the medicinal leech. When the model neuron and a heart interneuron are connected by inhibitory synapses, they produce rhythmic activity similar to that observed in the heartbeat network. We focused our studies on investigating the functional role of the hyperpolarization-activated inward current (I(h)) on the rhythmic bursts produced by the network. By introducing changes in both the model and the heart interneuron, we showed that I(h) determines both the period of rhythmic bursts and the balance of activity between the two sides of the network, because the amount and the activation/deactivation time constant of I(h) determines the length of time that a neuron spends in the inhibited phase of its burst cycle. Moreover, we demonstrated that the model neuron is an effective replacement for a heart interneuron and that changes made in the model can accurately mimic similar changes made in the living system. Finally, we used a previously developed mathematical model (Hill et al. 2001) of two mutually inhibitory interneurons to corroborate these findings. Our results demonstrated that this hybrid system technique is advantageous for investigating neuronal properties that are inaccessible with traditional techniques.

Figure 1.

Design and activity of hybrid half-center oscillator. A, Heart interneurons (HN), in an isolated ganglion preparation, were pharmacologically isolated with bicuculline. Voltage/current-clamp amplifiers were used for recording and current injection into heart interneurons and the silicon neuron (SiN). A single sharp microelectrode in discontinuous current-clamp mode was used for voltage recording and current injection into an isolated heart interneuron. Voltage recording and current injection into the silicon neuron were provided by direct connection to amplifier headstages (two-electrode current-clamp mode). Dynamic clamp provided real-time control signals to create artificial synapses between a heart interneuron and the silicon neuron. B, Activity of a living heart interneuron half-center oscillator in an isolated ganglion 3 (heart interneurons indexed by body side and ganglion number). C, Activity of a hybrid half-center oscillator.

Figure 2.

Steady-state activation and inactivation curves for the silicon neuron. The circles represent data from voltage clamp. Solid lines denote best fit of data to the activation/inactivation equations of Hill et al. (2001). The dashed lines show steady-state activation and inactivation curves for the currents of the canonical mathematical heart interneuron model. A, Fast sodium current (I_Na). B, Inactivating potassium current (I_K1). Data points from -75 to -45 mV are not shown because of large conductance/low current artifact. C, Slow, non-inactivating potassium current (I_K2). D, Slowly inactivating low-threshold calcium current (I_CaS). E, Persistent sodium current (I_P). F, Hyperpolarization-activated inward current (I_h).

Figure 3.

Activity of the silicon neuron depends on leak current parameters. A, Different types of activity, tonic spiking, bursting, and silence are expressed depending on the values of the leak reversal potential (E_leak) and the leak conductance (g_leak). The regions of silence and tonic spiking are separated by a region of intrinsic bursting. A small region, indicated in black (multistability), where bursting coexisted with tonic spiking was also observed. Inset, Similar activity map for the mathematical model of a heart interneuron (Cymbalyuk et al., 2002a). B, Typical activity of the silicon neuron when firing tonically. C, Typical activity of the silicon neuron when bursting intrinsically. Leak parameter values for the activity in B and C are indicated on the map in A.

Figure 4.

Dynamic-clamp-mediated inhibitory synapses of sufficient strength transform tonic firing into rhythmic antiphasic bursting in a hybrid half-center oscillator. A, Both the silicon neuron (SiN) and the pharmacologically isolated heart interneuron (HN) fire tonically in the absence of artificial synapses (ḡ_Syn = 0 nS). B, Weak artificial synapses (small ḡ_Syn) result in sporadic lapses in activity but not rhythmic bursting. C, Strong artificial synapses (large ḡ_Syn) result in stable alternating rhythmic bursting. The dashed line in A-C indicates -50 mV. D, Results of four experiments in which ḡ_Syn was varied between 0 and 625 nS. Different symbols represent different experiments. The period of rhythmic oscillations settle to a value that remains relatively unchanged with additional variations of ḡ_Syn. The error bars indicate the SD of the period over n ≥ 8 cycles for each trial of the four individual experiments.

Figure 5.

Strong artificial inhibitory synapses cause an immediate transition from tonic firing to rhythmic bursting in a hybrid half-center oscillator. Membrane potential, synaptic current (I_Syn), and h-current conductance (g_h) are shown for the silicon neuron (SiN) and the heart interneuron (HN). The vertical dashed line indicates the time at which the dynamic clamp was activated to enable the mutual inhibitory synapses. When one of the neurons is inhibited, its I_h activates, driving it back toward the firing threshold. Once it begins to fire, the other neuron is inhibited, its I_h activates, driving it back toward firing threshold so that it inhibits the first neuron, and the cycle repeats.

Figure 6.

Variation of ḡ_h in the silicon neuron (SiN ḡ_h) of a hybrid half-center oscillator. A, Typical activity at three different values of SiN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (SiN g_h) for the silicon neuron are shown. As SiN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered heart interneuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing SiN ḡ_h decreases the oscillator period. The period of the silicon neuron and the heart interneuron are the same. C, Increasing SiN ḡ_h decreases the burst duration of the heart interneuron, which is equivalent to the duration of the inhibited phase of the silicon neuron. D, Increasing SiN ḡ_h increases the final spike frequency of the heart interneuron, whereas the final spike frequency of silicon neuron remains relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying SiN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when SiN ḡ_h was at its smallest value (2 nS) in pairwise comparisons.

Figure 9.

A-C, ḡ_h determines when I_h reaches its maximal level of activation during the inhibited phase of the burst cycle of a hybrid half-center oscillator. We measured this timing as the percentage of the inhibited phase at which I_h achieved its maximal level of activation. A, SiN ḡ_h varied. B, HN ḡ_h varied in the presence of endogenous I_h. C, HN ḡ_h varied with endogenous I_h blocked by 2 mm Cs⁺. The data point at HN ḡ_h = 0 nS is rather fanciful because there is no endogenous h-current and none is added or subtracted with dynamic clamp. Thus, this point is not connected to the rest by a line segment. D, Changes in the oscillator period caused by variation of ḡ_h are primarily attributable to changes in burst duration of the non-modified “neuron” (equivalent to duration of the inactive phase in the modified neuron). The change in burst duration from the canonical operating point for the non-modified neuron is plotted versus the change in the oscillator period. The dashed line indicates that all of the change in the oscillator period is attributable to change in the burst duration of the non-modified neuron. The data points all lie near this line, indicating that I_h is selectively acting to shorten the inhibited phase of the burst cycle of the oscillator.

Figure 7.

Variation of ḡ_h in the heart interneuron (SiN ḡ_h) of a hybrid half-center oscillator with endogenous I_h present. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (HN g_h) for the heart interneuron are shown. As HN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered silicon neuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing HN ḡ_h decreases the oscillator period. The period of the silicon neuron and the heart interneuron are the same. C, Increasing HN ḡ_h decreases burst duration of the silicon neuron, which is equivalent to the duration of the inhibited phase of the heart interneuron. D, Increasing HN ḡ_h increases the final spike frequency of the silicon neuron, whereas the final spike frequency of the heart interneuron is relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying HN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when HN ḡ_h was at its smallest value (-12 nS) in pairwise comparisons.

Figure 8.

Variation of ḡ_h in the heart interneuron (HN ḡ_h) of a hybrid half-center oscillator with endogenous I_h blocked by 2 mm Cs⁺. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN), and h-current conductance (HN g_h) for the heart interneuron are shown. As HN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered silicon neuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing HN ḡ_h significantly decreases the oscillator period. The cycle period of the silicon neuron and the heart interneuron are the same. C, Increasing HN ḡ_h decreases the burst duration of the silicon neuron, which is equivalent to the duration of the inhibited phase of the heart interneuron. There is also a slight decrease in the burst duration of the heart interneuron. D, Increasing HN ḡ_h increases the final spike frequency of the silicon neuron, whereas the final spike frequency of the heart interneuron remains relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying HN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when HN ḡ_h was at its smallest value (0 nS).

Figure 10.

Unilateral variation of ḡ_h in the mathematical model of a heart interneuron half-center oscillator. A, Typical activity for an unbalanced half-center oscillator: membrane potential and h-current conductance (g_h) for both the varied (mHN_v) and the canonical (unvaried; mHN_c) model heart interneuron. B, Increasing ḡ_h causes a decrease in burst duration of the unvaried canonical “neuron,” which is equivalent to the duration of the inactive phase of the varied neuron. Varied neuron burst duration remains constant. Inset, Results for symmetric variation of ḡ_h plotted with the same axes values. C, Final spike frequency of unvaried canonical neuron increases with increasing ḡ_h. Final spike frequency of varied neuron remains relatively constant. Inset, Results for symmetric variation of ḡ_h plotted with the same axes values. The error bars indicate the SD over n ≥ 25 cycles for the individual modeling trial.

Figure 11.

Variation of τ_h in the silicon neuron (SiN τ_h) of a hybrid half-center oscillator. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (SiN g_h) for the heart interneuron are shown. The burst duration of the unaltered heart interneuron is indicated by brackets. B, Variations in SiN τ_h have a significant effect on the cycle period. Decreasing SiN τ_h, down to 0.5 sec, causes a decrease in the cycle period. An additional decrease in SiN τ_h, however, causes an increase in the cycle period. C, Decreasing SiN τ_h decreases the burst duration of the heart interneuron and also causes a slight decrease in the burst duration of the silicon neuron. D, Variations in SiN τ_h have no significant effect on the final spike frequency of either the silicon neuron or the heart interneuron. In B-D, a thick line connecting data points indicates a significant effect of varying SiNτ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when SiN τ_h was set at 0.5 sec in pairwise comparisons.