Interpreting posterior relative risk estimates in disease-mapping studies

Abstract

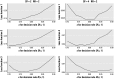
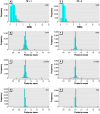
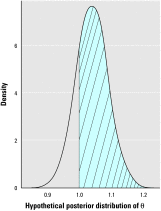
There is currently much interest in conducting spatial analyses of health outcomes at the small-area scale. This requires sophisticated statistical techniques, usually involving Bayesian models, to smooth the underlying risk estimates because the data are typically sparse. However, questions have been raised about the performance of these models for recovering the "true" risk surface, about the influence of the prior structure specified, and about the amount of smoothing of the risks that is actually performed. We describe a comprehensive simulation study designed to address these questions. Our results show that Bayesian disease-mapping models are essentially conservative, with high specificity even in situations with very sparse data but low sensitivity if the raised-risk areas have only a moderate (less than 2-fold) excess or are not based on substantial expected counts (> 50 per area). Semiparametric spatial mixture models typically produce less smoothing than their conditional autoregressive counterpart when there is sufficient information in the data (moderate-size expected count and/or high true excess risk). Sensitivity may be improved by exploiting the whole posterior distribution to try to detect true raised-risk areas rather than just reporting and mapping the mean posterior relative risk. For the widely used conditional autoregressive model, we show that a decision rule based on computing the probability that the relative risk is above 1 with a cutoff between 70 and 80% gives a specific rule with reasonable sensitivity for a range of scenarios having moderate expected counts (approximately 20) and excess risks (approximately 1.5- to 2-fold). Larger (3-fold) excess risks are detected almost certainly using this rule, even when based on small expected counts, although the mean of the posterior distribution is typically smoothed to about half the true value.

Figure B1. Variation of the total error rate (loss function) as function of the cutoff probability c for different weighting of the two types of errors (false positive and false negative). Results shown are for the Simu 2 using the BYM model.

Figure 1. Histograms of the raw SMRs (A,E ) and posterior means of the relative risks (B–H) for all the background areas of Simu 2 derived by each of the three models. Note that the crosses on the x-axes indicate the minimum and maximum values obtained. SF indicates the scale factor used for the expected values.

Figure 2. Histograms comparing the distribution of the posterior means of the relative risks estimated by the BYM or MIX models for the high-risk areas of Simu 2 or Simu 3 using a scale factor of 4 for the expected values and a true relative risk (marked by the vertical line on each plot) of θ = 2 (Simu 2) or θ *1=1.65 (Simu 3).

Figure 3. Box plots of the posterior means of the relative risks estimated by the three models for the high-risk areas of Simu 2 as a function of the scaling factor.

Figure 4. Posterior distribution of a relative risk θ, with shaded area indicating Prob(θ > 1).