Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly

Abstract

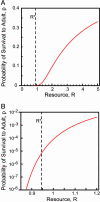
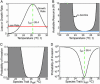
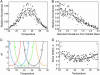
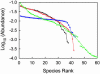
Stochastic niche theory resolves many of the differences between neutral theory and classical tradeoff-based niche theories of resource competition and community structure. In stochastic niche theory, invading species become established only if propagules can survive stochastic mortality while growing to maturity on the resources left unconsumed by established species. The theory makes three predictions about community structure. First, stochastic niche assembly creates communities in which species dominate approximately equally wide "slices" of the habitat's spatial heterogeneity. These niche widths generate realistic distributions of species relative abundances for which, contrary to neutral theory but consistent with numerous observations, there are strong correlations among species traits, species abundances, and environmental conditions. Second, slight decreases in resource levels are predicted to cause large decreases in the probability that a propagule would survive to be an adult. These decreases cause local diversity to be limited by the inhibitory effects of resource use by established species on the establishment (recruitment) of potential invaders. If resource pulses or disturbance allowed invaders to overcome this recruitment limitation, many more species could indefinitely coexist. Third, the low invasibility of high diversity communities is predicted to result not from diversity per se, but from the uniformly low levels of resources that occur in high-diversity communities created by stochastic competitive assembly. This prediction provides a potential solution to the invasion paradox, which is the tendency for highly diverse regions to be more heavily invaded.

Fig. 1.

Resource-dependent survival. (A) Effect of ambient resource levels on the probability (p; red curve) that a propagule would survive to become a reproductive adult (i.e., probability of invasion) based on Eq. 4. R* is the level to which an equilibrial population of the invading species would reduce the resource. (B) The same curve is shown, except that p is on a log scale, showing the large impacts on p of slight differences in R. Parameters were set as follows: m_p = 0.2 yr^–1, m_s = 0.4 yr^–1, B_s = 0.1, B_a = 10, K_i = 3, S_i = 1.0 yr^–1, and r_i = 5.0 yr^–1.

Fig. 2.

Gaussian growth, resource use, and invasion success. (A) Temperature-dependence of growth rate, g, based on Eq. 5. (B) The temperature- and resource-dependent zero net-growth isocline (black curve) of the species of A. The isocline shows the level to which R is reduced by an equilibrial population of this species. The shaded region shows resource levels available to potential invaders. (C) Dependence of probability of invasion (probability of propagule survival to adult) on the t_opt of an invader for the case illustrated in B. This function assumes that a propagule has landed in a site with its optimum temperature and that the established species is at equilibrium. (D) The same curve as in C but shown on a log scale. For these cases and those of Fig. 3, m_p = 0.2 yr^–1, m_s = 0.33 yr^–1, B_s = 0.05, B_a = 50, K_i = 2.5, S_i = 1.0 yr^–1, r_i = 5.0 yr^–1, σ_i = 2°C, and f = 10⁵. Species differ only in t_opt values.

Fig. 3.

Stochastic competitive assembly and resource use. An example of stochastic competitive assembly, based on simulation of Eqs. 1–5 for a case in which the temperature of a habitat and the t_opt of a propagule are both randomly drawn from uniform distributions on the temperature interval from 20°Cto30°C. Levels of available resources for the community after the second species becomes established (A, red isocline), after five species become established (B), and after 11 species become established (C; note the 10-fold change in scale for the y axis) in the community. Probabilities of subsequent invasion for the cases of A, B, and C, assuming that each species colonizes a site with a temperature equal to its t_opt. The two regions of high invasion probability for the two-species community (D) were the regions invaded by the next three species (E). The resources left unconsumed by the five-species community created zones with higher invasion probability (E; note 10-fold change in scale of y axis), which were the areas subsequently invaded (C and F; note 1,000-fold change in y axis for F).

Fig. 4.

Diversity and invasion. (A) Dynamics of species accumulation during stochastic competitive assembly shown for a simulation with Gaussian distributions of both habitat temperatures (mean, 25°C; σ = 2°C) and propagule t_opt values (mean, 25°C; σ = 2°C). Parameters were otherwise identical to those of Figs. 2 and 3, except that σ_i = 0.4°C. (Insert) Shown are three additional simulations differing only in the extent of habitat heterogeneity (σ), each illustrating that species number increases as the log of invasion events. (B) Log of the probability of future invasion (proportion of propagules that become established) declines linearly with species number. Results are for the same simulation shown in A.(C) Species number after 10⁶ invasion events for cases like those of A but with a range of values for B_s and B_a.

Fig. 5.

Results of stochastic competitive assembly. (A) Results of stochastic competitive assembly for five replicate simulations in which there were Gaussian distributions of both habitat temperatures and propagule t_opt values. Parameters equal those reported for Fig. 4 A and B. The distribution of relative abundances of habitat temperatures (solid curve) closely mimics the observed relative species abundances (points). (B) Relative abundance data of A graphed against the number of standard deviations of habitat heterogeneity (σ = 2°C) by which optimum temperatures of species differ from habitat mean temperature. The most abundant species are those with t_opt values corresponding to the most common habitat types. (C) Niche width is defined as the range of temperatures over which a species is the competitive dominant one. (D) Observed niche widths for the five simulations of A and B.

Fig. 6.

Stochastic competitive assembly and species abundances. Relative species abundance curves (average of five simulations, 10⁷ invasion events each) for four cases: Uniform distributions of both habitat temperature and t_opt values (blue; parameters equal those reported for Figs. 2 and 3, except that σ_i = 0.4°C); Gaussian habitat and uniform t_opt values (red; parameters equal those of the blue curve, but with habitat mean = 25°C and σ = 2°C); Gaussian habitat and Gaussian t_opt values [black (case shown in Figs. 4 and 5) and green (parameters equal those reported for Figs. 4 and 5, except that σ_i = 0.09°C with a habitat mean = 28.5°C and its σ = 2°C and a propagule t_opt mean = 21.5°C and its σ = 2.0°C)].