Tree-structured supervised learning and the genetics of hypertension
- PMID: 15249660
- PMCID: PMC489971
- DOI: 10.1073/pnas.0403794101
Tree-structured supervised learning and the genetics of hypertension
Abstract
This paper is about an algorithm, FlexTree, for general supervised learning. It extends the binary tree-structured approach (Classification and Regression Trees, CART) although it differs greatly in its selection and combination of predictors. It is particularly applicable to assessing interactions: gene by gene and gene by environment as they bear on complex disease. One model for predisposition to complex disease involves many genes. Of them, most are pure noise; each of the values that is not the prevalent genotype for the minority of genes that contribute to the signal carries a "score." Scores add. Individuals with scores above an unknown threshold are predisposed to the disease. For the additive score problem and simulated data, FlexTree has cross-validated risk better than many cutting-edge technologies to which it was compared when small fractions of candidate genes carry the signal. For the model where only a precise list of aberrant genotypes is predisposing, there is not a systematic pattern of absolute superiority; however, overall, FlexTree seems better than the other technologies. We tried the algorithm on data from 563 Chinese women, 206 hypotensive, 357 hypertensive, with information on ethnicity, menopausal status, insulin-resistant status, and 21 loci. FlexTree and Logic Regression appear better than the others in terms of Bayes risk. However, the differences are not significant in the usual statistical sense.
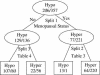
Figures
Similar articles
-
Evaluating the ability of tree-based methods and logistic regression for the detection of SNP-SNP interaction.Ann Hum Genet. 2009 May;73(Pt 3):360-9. doi: 10.1111/j.1469-1809.2009.00511.x. Epub 2009 Mar 8. Ann Hum Genet. 2009. PMID: 19291098
-
An optimal algorithm for perfect phylogeny haplotyping.J Comput Biol. 2006 May;13(4):897-928. doi: 10.1089/cmb.2006.13.897. J Comput Biol. 2006. PMID: 16761918
-
A partially linear tree-based regression model for assessing complex joint gene-gene and gene-environment effects.Genet Epidemiol. 2007 Apr;31(3):238-51. doi: 10.1002/gepi.20205. Genet Epidemiol. 2007. PMID: 17266115
-
An Empirical Bayes risk prediction model using multiple traits for sequencing data.Stat Appl Genet Mol Biol. 2015 Dec;14(6):551-73. doi: 10.1515/sagmb-2015-0060. Stat Appl Genet Mol Biol. 2015. PMID: 26641974
-
Detecting epistatic interactions contributing to quantitative traits.Genet Epidemiol. 2004 Sep;27(2):141-52. doi: 10.1002/gepi.20006. Genet Epidemiol. 2004. PMID: 15305330 Review.
Cited by
-
Two genetic variants in telomerase-associated protein 1 are associated with stomach cancer risk.J Hum Genet. 2016 Oct;61(10):885-889. doi: 10.1038/jhg.2016.71. Epub 2016 Jun 16. J Hum Genet. 2016. PMID: 27305982
-
Power of multifactor dimensionality reduction and penalized logistic regression for detecting gene-gene interaction in a case-control study.BMC Med Genet. 2009 Dec 4;10:127. doi: 10.1186/1471-2350-10-127. BMC Med Genet. 2009. PMID: 19961594 Free PMC article.
-
A prostate cancer model build by a novel SVM-ID3 hybrid feature selection method using both genotyping and phenotype data from dbGaP.PLoS One. 2014 Mar 20;9(3):e91404. doi: 10.1371/journal.pone.0091404. eCollection 2014. PLoS One. 2014. PMID: 24651484 Free PMC article.
-
Structures and Assumptions: Strategies to Harness Gene × Gene and Gene × Environment Interactions in GWAS.Stat Sci. 2009;24(4):472-488. doi: 10.1214/09-sts287. Stat Sci. 2009. PMID: 20640184 Free PMC article.
-
SNPs and other features as they predispose to complex disease: genome-wide predictive analysis of a quantitative phenotype for hypertension.PLoS One. 2011;6(11):e27891. doi: 10.1371/journal.pone.0027891. Epub 2011 Nov 30. PLoS One. 2011. PMID: 22140480 Free PMC article.
References
-
- Breiman, L., Friedman, J. H., Olshen, R. A. & Stone, C. J. (1984) Classification and Regression Trees (Wadsworth, Belmont, CA), 1st Ed.
-
- Zhang, H. (1998) J. Am. Stat. Assoc. 93, 180–193.
-
- Zhang, H. & Bonney, G. (2000) Genet. Epidemiol. 19, 323–332. - PubMed
-
- Tibshirani, R., Hastie, T. & Buja, A. (1995) Ann. Stat. 23, 73–102.
-
- Hastie, T., Friedman, J. H. & Tibshirani, R. (2001) The Elements of Statistical Learning: Data Mining, Inference and Prediction (Springer, New York), 1st Ed.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

