A force-dependent switch reverses type IV pilus retraction
- PMID: 15256598
- PMCID: PMC503726
- DOI: 10.1073/pnas.0402305101
A force-dependent switch reverses type IV pilus retraction
Abstract
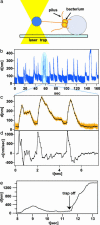
Type IV pilus dynamics is important for virulence, motility, and DNA transfer in a wide variety of prokaryotes. The type IV pilus system constitutes a very robust and powerful molecular machine that transports pilus polymers as well as DNA through the bacterial cell envelope. In Neisseria gonorrhoeae, pilus retraction is a highly irreversible process that depends on PilT, an AAA ATPase family member. However, when levels of PilT are reduced, the application of high external forces (F = 110 +/- 10 pN) induces processive pilus elongation. At forces of >50 pN, single pili elongate at a rate of v = 350 +/- 50 nm/s. For forces of <50 pN, elongation velocity depends strongly on force and relaxation causes immediate retraction. Both pilus retraction and force-induced elongation can be modeled by chemical kinetics with same step length for the rate-limiting translocation step. The model implies that a force-dependent molecular switch can induce pilus elongation by reversing the retraction mechanism.
Figures



References
-
- Merz, A. J. & So, M. (2000) Annu. Rev. Cell Dev. Biol. 16, 423–457. - PubMed
-
- Aas, F. E., Wolfgang, M., Frye, S., Dunham, S., Lovold, C. & Koomey, M. (2002) Mol. Microbiol. 46, 749–760. - PubMed
-
- Merz, A. J., So, M. & Sheetz, M. P. (2000) Nature 407, 98–102. - PubMed
-
- Kaiser, D. (2000) Curr. Biol. 10, R777–R780. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

