Transparallel processing by hyperstrings
- PMID: 15263075
- PMCID: PMC503711
- DOI: 10.1073/pnas.0403402101
Transparallel processing by hyperstrings
Abstract
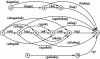
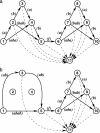
Human vision research aims at understanding the brain processes that enable us to see the world as a structured whole consisting of separate objects. To explain how humans organize a visual pattern, structural information theory starts from the idea that our visual system prefers the organization with the simplest descriptive code, that is, the code that captures a maximum of visual regularity. Empirically, structural information theory gained support from psychological data on a wide variety of perceptual phenomena, but theoretically, the computation of guaranteed simplest codes remained a troubling problem. Here, the graph-theoretical concept of "hyperstrings" is presented as a key to the solution of this problem. A hyperstring is a distributed data structure that allows a search for regularity in O(2(N)) strings as if only one string of length N were concerned. Thereby, hyperstrings enable transparallel processing, a previously uncharacterized form of processing that might also be a form of cognitive processing.
Figures

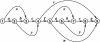



Similar articles
-
Cognitive architecture of perceptual organization: from neurons to gnosons.Cogn Process. 2012 Feb;13(1):13-40. doi: 10.1007/s10339-011-0425-9. Epub 2011 Nov 16. Cogn Process. 2012. PMID: 22086351 Free PMC article. Review.
-
Proceedings of the Second Workshop on Theory meets Industry (Erwin-Schrödinger-Institute (ESI), Vienna, Austria, 12-14 June 2007).J Phys Condens Matter. 2008 Feb 13;20(6):060301. doi: 10.1088/0953-8984/20/06/060301. Epub 2008 Jan 24. J Phys Condens Matter. 2008. PMID: 21693862
-
Orthographic regularity, positional frequency, and visual processing of letter strings.J Exp Psychol Gen. 1979 Mar;108(1):107-24. J Exp Psychol Gen. 1979. PMID: 528895
-
Orthographic regularity, lexical status, and letter-identification acuity.Percept Mot Skills. 1982 Oct;55(2):635-47. doi: 10.2466/pms.1982.55.2.635. Percept Mot Skills. 1982. PMID: 7155759
-
Disorders of visual recognition.Semin Neurol. 2000;20(4):479-85. doi: 10.1055/s-2000-13181. Semin Neurol. 2000. PMID: 11149704 Review.
Cited by
-
Cognitive architecture of perceptual organization: from neurons to gnosons.Cogn Process. 2012 Feb;13(1):13-40. doi: 10.1007/s10339-011-0425-9. Epub 2011 Nov 16. Cogn Process. 2012. PMID: 22086351 Free PMC article. Review.
-
A century of Gestalt psychology in visual perception: II. Conceptual and theoretical foundations.Psychol Bull. 2012 Nov;138(6):1218-52. doi: 10.1037/a0029334. Epub 2012 Jul 30. Psychol Bull. 2012. PMID: 22845750 Free PMC article. Review.
-
Aesthetic Responses to Exact Fractals Driven by Physical Complexity.Front Hum Neurosci. 2016 May 20;10:210. doi: 10.3389/fnhum.2016.00210. eCollection 2016. Front Hum Neurosci. 2016. PMID: 27242475 Free PMC article.
-
Structural coding versus free-energy predictive coding.Psychon Bull Rev. 2016 Jun;23(3):663-77. doi: 10.3758/s13423-015-0938-9. Psychon Bull Rev. 2016. PMID: 26407895 Review.
-
Dubious Claims about Simplicity and Likelihood: Comment on Pinna and Conti (2019).Brain Sci. 2020 Jan 16;10(1):50. doi: 10.3390/brainsci10010050. Brain Sci. 2020. PMID: 31963341 Free PMC article.
References
-
- Leeuwenberg, E. L. J. (1968) Structural Information of Visual Patterns: An Efficient Coding System in Perception (Mouton, The Hague, The Netherlands).
-
- Hochberg, J. E. & McAlister, E. (1953) J. Exp. Psychol. 46, 361–364. - PubMed
-
- Shannon, C. E. (1948) Bell System Tech. J. 27, 379–423, 623–656.
-
- Koffka, K. (1935) Principles of Gestalt Psychology (Routledge & Kegan Paul, London).
-
- van der Helm, P. A., van Lier, R. & Wagemans, J., eds. (2003) Visual Gestalt Formation, special issue of Acta Psychol. 114, 211–398.
LinkOut - more resources
Full Text Sources

