Modular decomposition of protein-protein interaction networks
- PMID: 15287979
- PMCID: PMC507882
- DOI: 10.1186/gb-2004-5-8-r57
Modular decomposition of protein-protein interaction networks
Abstract
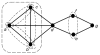
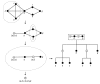
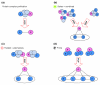
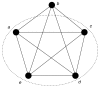
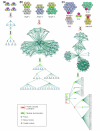
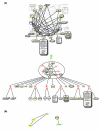
We introduce an algorithmic method, termed modular decomposition, that defines the organization of protein-interaction networks as a hierarchy of nested modules. Modular decomposition derives the logical rules of how to combine proteins into the actual functional complexes by identifying groups of proteins acting as a single unit (sub-complexes) and those that can be alternatively exchanged in a set of similar complexes. The method is applied to experimental data on the pro-inflammatory tumor necrosis factor-alpha (TNF-alpha)/NFkappaB transcription factor pathway.
Figures
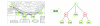
References
-
- Deng M, Sun F, Chen T. Assessment of the reliability of protein-protein interactions and protein function prediction. Pac Symp Biocomput. 2003:140–151. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

