Bayesian analysis of botanical epidemics using stochastic compartmental models

Abstract

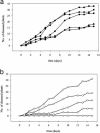
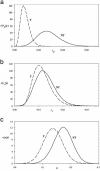
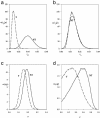
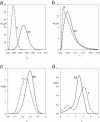
A stochastic model for an epidemic, incorporating susceptible, latent, and infectious states, is developed. The model represents primary and secondary infection rates and a time-varying host susceptibility with applications to a wide range of epidemiological systems. A Markov chain Monte Carlo algorithm is presented that allows the model to be fitted to experimental observations within a Bayesian framework. The approach allows the uncertainty in unobserved aspects of the process to be represented in the parameter posterior densities. The methods are applied to experimental observations of damping-off of radish (Raphanus sativus) caused by the fungal pathogen Rhizoctonia solani, in the presence and absence of the antagonistic fungus Trichoderma viride, a biological control agent that has previously been shown to affect the rate of primary infection by using a maximum-likelihood estimate for a simpler model with no allowance for a latent period. Using the Bayesian analysis, we are able to estimate the latent period from population data, even when there is uncertainty in discriminating infectious from latently infected individuals in data collection. We also show that the inference that T. viride can control primary, but not secondary, infection is robust to inclusion of the latent period in the model, although the absolute values of the parameters change. Some refinements and potential difficulties with the Bayesian approach in this context, when prior information on parameters is lacking, are discussed along with broader applications of the methods to a wide range of epidemiological systems.

Fig. 1.

Disease progress curves for epidemics of damping-off caused by R. solani in five replicate microcosms of radish in the absence (a) and presence (b) of the biological control agent T. viride.

Fig. 2.

Marginal posterior densities, estimated by MCMC, for individual parameters of the SEI model (with latent period μ set to zero) for replicated epidemics in the presence and absence of the biological control agent. T. viride. (a) Primary infection rate, r_p. (b) Secondary infection rate, r_s. (c) Susceptibility decay, a. T, Trichoderma present; NT, Trichoderma absent.

Fig. 3.

Marginal posterior densities, estimated by MCMC, for individual parameters of the SEI model for replicated epidemics in the presence and absence of the biological control agent T. viride, assuming that only plants in class I are recorded as diseased. (a) Primary infection rate, r_p. (b) Secondary infection rate, r_s. (c) Susceptibility decay, a. (d) Latent period, μ.T, Trichoderma present; NT, Trichoderma absent.

Fig. 4.

Marginal posterior densities, estimated by MCMC, for individual parameters of the SEI model for replicated epidemics in the presence and absence of the biological control agent T. viride, assuming that plants in class I and plants in class E are recorded as diseased. (a) Primary infection rate, r_p. (b) Secondary infection rate, r_s. (c) Susceptibility decay, a. (d) Latent period, μ. T, Trichoderma present; NT, Trichoderma absent.