Ecological theory suggests that antimicrobial cycling will not reduce antimicrobial resistance in hospitals
- PMID: 15308772
- PMCID: PMC516561
- DOI: 10.1073/pnas.0402298101
Ecological theory suggests that antimicrobial cycling will not reduce antimicrobial resistance in hospitals
Abstract
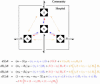
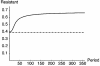
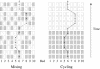
Hospital-acquired infections caused by antibiotic-resistant bacteria pose a grave and growing threat to public health. Antimicrobial cycling, in which two or more antibiotic classes are alternated on a time scale of months to years, seems to be a leading candidate in the search for treatment strategies that can slow the evolution and spread of antibiotic resistance in hospitals. We develop a mathematical model of antimicrobial cycling in a hospital setting and use this model to explore the efficacy of cycling programs. We find that cycling is unlikely to reduce either the evolution or the spread of antibiotic resistance. Alternative drug-use strategies such as mixing, in which each treated patient receives one of several drug classes used simultaneously in the hospital, are predicted to be more effective. A simple ecological explanation underlies these results. Heterogeneous antibiotic use slows the spread of resistance. However, at the scale relevant to bacterial populations, mixing imposes greater heterogeneity than does cycling. As a consequence, cycling is unlikely to be effective and may even hinder resistance control. These results may explain the limited success reported thus far from clinical trials of antimicrobial cycling.
Figures

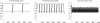


Comment in
-
Cycling antibiotics may not be good for your health.Proc Natl Acad Sci U S A. 2004 Sep 7;101(36):13101-2. doi: 10.1073/pnas.0404970101. Epub 2004 Aug 30. Proc Natl Acad Sci U S A. 2004. PMID: 15340145 Free PMC article. No abstract available.
References
-
- Niederman, M. S. (2001) Crit. Care Med. 29, Suppl., N114-N120. - PubMed
-
- Zaidi, M., Sifuentes-Osornio, J., Rolon, A. L., Vazquez, G., Rosado, R., Sanchez, M., Calva, J. J. & de Leon-Rosales, S. P. (2002) Arch. Med. Res. 33, 290-294. - PubMed
-
- Kollef, M. H. & Fraser, V. J. (2001) Ann. Intern. Med. 134, 298-314. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

