A semianalytic model of leukocyte rolling

Abstract

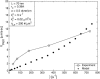
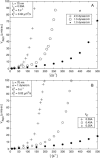
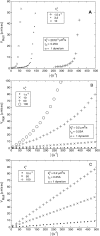
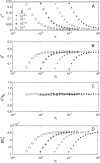
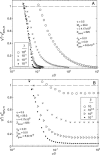
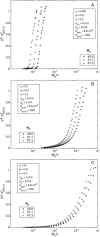
Rolling allows leukocytes to maintain adhesion to vascular endothelium and to molecularly coated surfaces in flow chambers. Using insights from adhesive dynamics, a computational method for simulating leukocyte rolling and firm adhesion, we have developed a semianalytic model for the steady-state rolling of a leukocyte. After formation in a force-free region of the contact zone, receptor-ligand bonds are transported into the trailing edge of the contact zone. Rolling velocity results from a balance of the convective flux of bonds and the rate of dissociation at the back edge of the contact zone. We compare the model's results to that of adhesive dynamics and to experimental data on the rolling of leukocytes, with good agreement. We calculate the dependence of rolling velocity on shear rate, intrinsic forward and reverse reaction rates, bond stiffness, and reactive compliance, and use the model to calculate a state diagram relating molecular parameters and the dynamic state of adhesion. A dimensionless form of the analytic model permits exploration of the parameters that control rolling. The chemical affinity of a receptor-ligand pair does not uniquely determine rolling velocity. We elucidate a fundamental relationship between off-rate, ligand density, and reactive compliance at the transition between firm and rolling adhesion. The model provides a rapid method for screening system parameters for the potential to mediate rolling.

FIGURE 1

Schematic diagram of the semianalytic model. The contact zone of radius L is at separation distance H₀ from the wall. H_max and H_min are distances at which the reverse reaction rate, k_r, is 100 and 2 times the intrinsic rate, respectively. The contact zone is divided into leading and trailing zones where y = H_min, or x = −L + δ. The bonds in the trailing zone, simplified as a homogenous population of “average” bonds, exert tension at the midpoint between the x coordinates corresponding to H_max and H_min.

FIGURE 2

Dimensional results comparable to experimental data of Lawrence and Springer (1991) for neutrophils rolling over P-selectin coated surfaces. Solid markers represent model results with PSGL-1 site density on the neutrophil surface (n_RT = 48 #/μm²) taken from Rodgers et al. (2000). Open markers represent experimental data. Parameter values are indicated in legends.

FIGURE 3

Dimensional rolling velocity as a function of shear rate at several values of σ, the bond spring constant (A) and of r_C, the reactive compliance (B). n_RT = 48 #/μm², n_LT = 200 #/μm², ξ = 5 × 10⁻⁴ dyne, and λ = 70 nm.

FIGURE 4

Dimensional rolling velocity as a function of shear rate at various for (A) (B) and (C) n_LT = 100 #/μm², ξ = 5 × 10⁻⁴ dyne, and λ = 70 nm.

FIGURE 5

Adhesion state diagrams. (A) Semianalytic model dimensional state diagram with intrinsic reverse reaction rate, plotted versus r_C, reactive compliance, for bond spring constant, σ, values of 2.5 and 1 dyne/cm. Solid lines enclose rolling state phase space. Open markers correspond to Bell model parameters for various selectins and their ligands, cataloged in Chang et al. (2000). (B) Adhesive dynamics state diagram. The upper and lower boundaries of the transient adhesion state delimit fractional stop times of 0.01 and 0.7, respectively. A mean velocity of 0.5 V_H parameterizes the upper boundary of the fast adhesion state, and the dotted and dashed lines correspond to 0.3 V_H and 0.1 V_H, respectively. Open markers correspond to Bell model parameters for various selectins and their ligands. (Reproduced with permission; Chang et al., 2000).

FIGURE 6

Dimensionless steady-state rolling velocity V* (A), contact angle θ* (B), separation distance scaled by dimensionless equilibrium bond length h*/δ_B (C), and trailing zone bond density output BD₂* (D) as a function of η, ratio of receptor to ligand densities. Upper and lower dashed lines in A indicate 0.5 V_H and 0.01 V_H, respectively. The curves are parameterized by β, the dimensionless reverse reaction rate, which increases from left to right. The rolling velocity is anti-correlated with BD₂*. M₀ = 87.6, χ = 0.2, ν = 1.2 × 10⁶, Z_bond = 9.38 × 10³, Z_grav = 4.1 × 10⁻⁵, δ_B = 0.01, and δ_SS = 0.01.

FIGURE 7

State diagram depicting the β-χ boundary between rolling and firm adhesion. (β is the dimensionless reverse reaction rate, and χ is the dimensionless forward reaction rate.) The solid line corresponds to dimensionless parameters in the upper left corner of the figure. Other lines represent boundaries resulting from replacement of an individual parameter with an indicated value. All curves have the same characteristic shape, where β is independent of χ at high χ, but β is proportional to χ at low χ.

FIGURE 8

Dependence of rolling velocity on chemical affinity. Rolling velocity, normalized to 50% of the hydrodynamic velocity (V_50%H) as a function of χ/β for several values of constant β (A) and constant χ (B). Upper and lower dashed lines indicate 0.01 V_H and 0.5 V_H, respectively. Chemical affinity does not determine a unique rolling velocity; for one value of χ/β, a range of rolling velocities exists. Conversely, rolling velocity does not require a unique chemical affinity; one value of rolling velocity can be achieved by many χ/β. At high chemical affinity, χ/β, rolling velocity is determined by β.

FIGURE 9

State diagram depicting the β-ν/M₀ boundary between rolling and firm adhesion. The solid line corresponds to dimensionless parameters in the upper left corner of the figure. Other lines represent boundaries resulting from replacement of an individual parameter with an indicated value. Surprisingly, β is proportional to ν/M₀ for all parameter values, leading to a unique scaling for the onset of rolling adhesion.

FIGURE 10

Dimensionless rolling velocity, normalized to 50% V_H, as a function of M₀/ν, for three values of dimensionless forward rate, χ: (A) 0.002, (B) 0.2, and (C) 20. Results for various values of M₀, the ratio of bond-spring energy to thermal energy, appear in each subplot.