Michaelis-Menten kinetics under spatially constrained conditions: application to mibefradil pharmacokinetics

Abstract

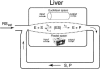
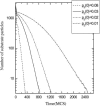
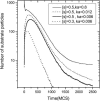
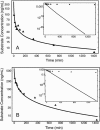
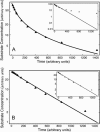
Two different approaches were used to study the kinetics of the enzymatic reaction under heterogeneous conditions to interpret the unusual nonlinear pharmacokinetics of mibefradil. Firstly, a detailed model based on the kinetic differential equations is proposed to study the enzymatic reaction under spatial constraints and in vivo conditions. Secondly, Monte Carlo simulations of the enzyme reaction in a two-dimensional square lattice, placing special emphasis on the input and output of the substrate were applied to mimic in vivo conditions. Both the mathematical model and the Monte Carlo simulations for the enzymatic reaction reproduced the classical Michaelis-Menten (MM) kinetics in homogeneous media and unusual kinetics in fractal media. Based on these findings, a time-dependent version of the classic MM equation was developed for the rate of change of the substrate concentration in disordered media and was successfully used to describe the experimental plasma concentration-time data of mibefradil and derive estimates for the model parameters. The unusual nonlinear pharmacokinetics of mibefradil originates from the heterogeneous conditions in the reaction space of the enzymatic reaction. The modified MM equation can describe the pharmacokinetics of mibefradil as it is able to capture the heterogeneity of the enzymatic reaction in disordered media.

FIGURE 1

A microscopic model for the enzymatic reaction in the liver. The topology of the reaction space in the liver can be considered either Euclidean or fractal. RS_ext denotes the rate of substrate input.

FIGURE 2

A 50 × 50 percolation fractal. Only the largest cluster is shown. Particles are allowed to move on the white sites only. Black sites are restricted area obstacles. Substrate molecules enter to the lattice from randomly chosen white sites labeled as entrances.

FIGURE 3

Plot of p_S versus time using the microscopic model of the enzymatic reaction. Points are experimental in vivo data from Fuite et al. (2002). The solid line represents results of the numerical solution of the system of Eqs. 3–5 assuming fractal kinetics (i.e., Eq. 6) combined with a Levenberg-Marquardt fitting algorithm. The fitted results are rescaled to change to actual units. Rescaling factors are also determined by Levenberg-Marquardt fitting.

FIGURE 4

Semilog plot of p_S versus time for several initial values of enzyme concentration, p_E, in a Euclidean space (zero density of obstacles) using MC simulation. We assume injection-type drug delivery, i.e., at t = 0 all drug molecules are supposed to be in the lattice, randomly distributed. The values assumed for the reaction probabilities are f = 1, r = 0.02, and g = 0.04. The initial substrate concentration was set to p_s = 0.2.

FIGURE 5

MC simulations using the “largest-cluster model”. Semilog plot of p_S versus time assuming delivery of the drug through first-order kinetics for several values of the first-order constant, k_a, and two levels of the initial substrate concentration. The values assumed for the reaction probabilities are f = 1, r = 0.02, and g = 0.04 and the initial enzyme concentration is p_e = 0.06.

FIGURE 6

Plot of p_S versus time. Points are experimental in vivo data from Fuite et al. (2002). Dashed line represents MCS results using the “all-clusters model”. The values assumed for the reaction probabilities are f = 1, r = 0.02, and g = 0.04. The following parameters have given the best fitting results: p_s(0) = 0.2, p_e(0) = 0.2, T = 48, σ = 12. Thin solid line represents MCS results using the “largest-cluster model”. The following parameters have given the best fitting results: f = 1, r = 0.015, g = 0.02, ps(0) = 0.6, p_e(0) = 0.2, T = 48, σ = 10. We rescale to change from Monte Carlo units to actual time units. Rescaling factors are determined by Levenberg-Marquardt fitting. In both cases it turns out that 1 min = 0.88 MC steps.

FIGURE 7

Semilogarithmic concentration (p_s) versus time plots of mibefradil after intravenous bolus administration. Data were taken from reference Fuite et al. (2002) (A), and reference Skerjanec et al. (1996) (B). The solid lines represent the fittings of Eqs. 2 (A and B insets) and 7 (A and B) to experimental data.

FIGURE 8

Semilogarithmic concentration (p_s) versus time plots for data generated from one-compartment model with first-order input and elimination based on Eq. 7. The parameter values (in arbitrary units) used for the generation of data are: V_m = 0.4, K_m0 = 0.2, h = 1.0, dose X₀ = 100, and either a high 1.0 (A) or low 0.01 (B) value for the absorption rate constant. The lines represent the fitting results of the two models: classic MM (A and B insets) and fractal model (A and B) to data.