A model of effective diffusion and tortuosity in the extracellular space of the brain
- PMID: 15345540
- PMCID: PMC1304566
- DOI: 10.1529/biophysj.103.039495
A model of effective diffusion and tortuosity in the extracellular space of the brain
Abstract
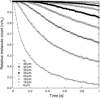
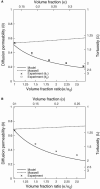
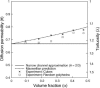
Tortuosity of the extracellular space describes hindrance posed to the diffusion process by a geometrically complex medium in comparison to an environment free of any obstacles. Calculating tortuosity in biologically relevant geometries is difficult. Yet this parameter has proved very important for many processes in the brain, ranging from ischemia and osmotic stress to delivery of nutrients and drugs. It is also significant for interpretation of the diffusion-weighted magnetic resonance data. We use a volume-averaging procedure to obtain a general expression for tortuosity in a complex environment. A simple approximation then leads to tortuosity estimates in a number of two-dimensional (2D) and three-dimensional (3D) geometries characterized by narrow pathways between the cellular elements. It also explains the counterintuitive fact of lower diffusion hindrance in a 3D environment. Comparison with Monte Carlo numerical simulations shows that the model gives reasonable tortuosity estimates for a number of regular and randomized 2D and 3D geometries. Importantly, it is shown that addition of dead-end pores increases tortuosity in proportion to the square root of enlarged total extracellular volume fraction. This conclusion is further supported by the previously described tortuosity decrease in ischemic brain slices where dead-end pores were partially occluded by large macromolecules introduced into the extracellular space.
Figures



Similar articles
-
Maximum geometrical hindrance to diffusion in brain extracellular space surrounding uniformly spaced convex cells.J Theor Biol. 2004 Jul 7;229(1):59-68. doi: 10.1016/j.jtbi.2004.03.003. J Theor Biol. 2004. PMID: 15178185
-
Cell cavities increase tortuosity in brain extracellular space.J Theor Biol. 2005 Jun 21;234(4):525-36. doi: 10.1016/j.jtbi.2004.12.009. J Theor Biol. 2005. PMID: 15808873
-
Contribution of dead-space microdomains to tortuosity of brain extracellular space.Neurochem Int. 2004 Sep;45(4):467-77. doi: 10.1016/j.neuint.2003.11.011. Neurochem Int. 2004. PMID: 15186912 Review.
-
Diffusion of molecules in brain extracellular space: theory and experiment.Prog Brain Res. 2000;125:129-54. doi: 10.1016/S0079-6123(00)25007-3. Prog Brain Res. 2000. PMID: 11098654 Review.
-
Geometric and viscous components of the tortuosity of the extracellular space in the brain.Proc Natl Acad Sci U S A. 1998 Jul 21;95(15):8975-80. doi: 10.1073/pnas.95.15.8975. Proc Natl Acad Sci U S A. 1998. PMID: 9671789 Free PMC article.
Cited by
-
Improving the Prediction of Local Drug Distribution Profiles in the Brain with a New 2D Mathematical Model.Bull Math Biol. 2019 Sep;81(9):3477-3507. doi: 10.1007/s11538-018-0469-4. Epub 2018 Aug 8. Bull Math Biol. 2019. PMID: 30091104 Free PMC article.
-
Organotypic whole hemisphere brain slice models to study the effects of donor age and oxygen-glucose-deprivation on the extracellular properties of cortical and striatal tissue.J Biol Eng. 2022 Jun 13;16(1):14. doi: 10.1186/s13036-022-00293-w. J Biol Eng. 2022. PMID: 35698088 Free PMC article.
-
Gliotoxin-induced swelling of astrocytes hinders diffusion in brain extracellular space via formation of dead-space microdomains.Glia. 2014 Jul;62(7):1053-65. doi: 10.1002/glia.22661. Epub 2014 Mar 31. Glia. 2014. PMID: 24687699 Free PMC article.
-
Diffusion of flexible random-coil dextran polymers measured in anisotropic brain extracellular space by integrative optical imaging.Biophys J. 2008 Aug;95(3):1382-92. doi: 10.1529/biophysj.107.124743. Epub 2008 May 2. Biophys J. 2008. PMID: 18456831 Free PMC article.
-
Enlarged extracellular space of aquaporin-4-deficient mice does not enhance diffusion of Alexa Fluor 488 or dextran polymers.Neuroscience. 2009 Jun 16;161(1):39-45. doi: 10.1016/j.neuroscience.2009.03.017. Epub 2009 Mar 19. Neuroscience. 2009. PMID: 19303428 Free PMC article.
References
-
- Barber, C. B., D. P. Dobkin, and H. T. Huhdanpaa. 1996. The Quickhull algorithm for convex hulls. ACM Trans. Math. Software. 22:469–483.
-
- Callaghan, P. T. 1991. Principles of Nuclear Magnetic Resonance Microscopy, 1st Ed. Clarendon Press, Oxford, UK.
-
- Crank, 1975. The Mathematics of Diffusion, 2nd Ed. Oxford University Press, New York, NY.
-
- Einstein, A. 1956. Investigations on the Theory of the Brownian Movement, 1st Ed. Dover, New York, NY.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

