A model of effective diffusion and tortuosity in the extracellular space of the brain
- PMID: 15345540
- PMCID: PMC1304566
- DOI: 10.1529/biophysj.103.039495
A model of effective diffusion and tortuosity in the extracellular space of the brain
Abstract
Tortuosity of the extracellular space describes hindrance posed to the diffusion process by a geometrically complex medium in comparison to an environment free of any obstacles. Calculating tortuosity in biologically relevant geometries is difficult. Yet this parameter has proved very important for many processes in the brain, ranging from ischemia and osmotic stress to delivery of nutrients and drugs. It is also significant for interpretation of the diffusion-weighted magnetic resonance data. We use a volume-averaging procedure to obtain a general expression for tortuosity in a complex environment. A simple approximation then leads to tortuosity estimates in a number of two-dimensional (2D) and three-dimensional (3D) geometries characterized by narrow pathways between the cellular elements. It also explains the counterintuitive fact of lower diffusion hindrance in a 3D environment. Comparison with Monte Carlo numerical simulations shows that the model gives reasonable tortuosity estimates for a number of regular and randomized 2D and 3D geometries. Importantly, it is shown that addition of dead-end pores increases tortuosity in proportion to the square root of enlarged total extracellular volume fraction. This conclusion is further supported by the previously described tortuosity decrease in ischemic brain slices where dead-end pores were partially occluded by large macromolecules introduced into the extracellular space.
Figures
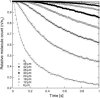

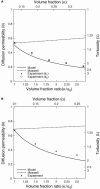
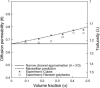


References
-
- Barber, C. B., D. P. Dobkin, and H. T. Huhdanpaa. 1996. The Quickhull algorithm for convex hulls. ACM Trans. Math. Software. 22:469–483.
-
- Callaghan, P. T. 1991. Principles of Nuclear Magnetic Resonance Microscopy, 1st Ed. Clarendon Press, Oxford, UK.
-
- Crank, 1975. The Mathematics of Diffusion, 2nd Ed. Oxford University Press, New York, NY.
-
- Einstein, A. 1956. Investigations on the Theory of the Brownian Movement, 1st Ed. Dover, New York, NY.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

