Model-based fitting of single-channel dwell-time distributions
- PMID: 15345545
- PMCID: PMC1304571
- DOI: 10.1529/biophysj.103.037531
Model-based fitting of single-channel dwell-time distributions
Abstract
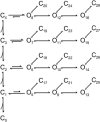
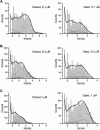
Single-channel recordings provide unprecedented resolutions on kinetics of conformational changes of ion channels. Several approaches exist for analysis of the data, including the dwell-time histogram fittings and the full maximal-likelihood approaches that fit either the idealized dwell-time sequence or more ambitiously the noisy data directly using hidden Markov modeling. Although the full maximum likelihood approaches are statistically advantageous, they can be time-consuming especially for large datasets and/or complex models. We present here an alternative approach for model-based fitting of one-dimensional and two-dimensional dwell-time histograms. To improve performance, we derived analytical expressions for the derivatives of one-dimensional and two-dimensional dwell-time distribution functions and employed the gradient-based variable metric method for fast search of optimal rate constants in a model. The algorithm also has the ability to allow for a first-order correction for the effects of missed events, global fitting across different experimental conditions, and imposition of typical constraints on rate constants including microscopic reversibility. Numerical examples are presented to illustrate the performance of the algorithm, and comparisons with the full maximum likelihood fitting are discussed.
Figures









Similar articles
-
A direct optimization approach to hidden Markov modeling for single channel kinetics.Biophys J. 2000 Oct;79(4):1915-27. doi: 10.1016/S0006-3495(00)76441-1. Biophys J. 2000. PMID: 11023897 Free PMC article.
-
Hidden Markov modeling for single channel kinetics with filtering and correlated noise.Biophys J. 2000 Oct;79(4):1928-44. doi: 10.1016/S0006-3495(00)76442-3. Biophys J. 2000. PMID: 11023898 Free PMC article.
-
Rapid kinetic analysis of multichannel records by a simultaneous fit to all dwell-time histograms.Biophys J. 2000 Feb;78(2):785-99. doi: 10.1016/S0006-3495(00)76636-7. Biophys J. 2000. PMID: 10653791 Free PMC article.
-
Principles of single-channel kinetic analysis.Methods Mol Biol. 2007;403:253-86. doi: 10.1007/978-1-59745-529-9_17. Methods Mol Biol. 2007. PMID: 18828000 Review.
-
Cooperative gating between ion channels.Gen Physiol Biophys. 2014;33(1):1-12. doi: 10.4149/gpb_2013076. Epub 2013 Oct 31. Gen Physiol Biophys. 2014. PMID: 24177017 Review.
Cited by
-
The fractal brain: scale-invariance in structure and dynamics.Cereb Cortex. 2023 Apr 4;33(8):4574-4605. doi: 10.1093/cercor/bhac363. Cereb Cortex. 2023. PMID: 36156074 Free PMC article. Review.
-
Probing RNA structure and interaction dynamics at the single molecule level.Methods. 2019 Jun 1;162-163:3-11. doi: 10.1016/j.ymeth.2019.04.002. Epub 2019 Apr 3. Methods. 2019. PMID: 30951833 Free PMC article. Review.
-
Effects of ethanol on GluN1/GluN2A and GluN1/GluN2B NMDA receptor-ion channel gating kinetics.Alcohol Clin Exp Res. 2022 Dec;46(12):2203-2213. doi: 10.1111/acer.14965. Epub 2022 Nov 9. Alcohol Clin Exp Res. 2022. PMID: 36305341 Free PMC article.
-
2D-dwell-time analysis with simulations of ion-channel gating using high-performance computing.Biophys J. 2023 Apr 4;122(7):1287-1300. doi: 10.1016/j.bpj.2023.02.023. Epub 2023 Feb 22. Biophys J. 2023. PMID: 36814379 Free PMC article.
-
Dynamic competition between a ligand and transcription factor NusA governs riboswitch-mediated transcription regulation.Proc Natl Acad Sci U S A. 2021 Nov 23;118(47):e2109026118. doi: 10.1073/pnas.2109026118. Proc Natl Acad Sci U S A. 2021. PMID: 34782462 Free PMC article.
References
-
- Ball, F. G., and M. S. P. Sansom. 1989. Ion-channel gating mechanisms: model identification and parameter estimation from single channel recordings. Proc. R. Soc. Lond. B Biol. Sci. 236:385–416. - PubMed
-
- Colquhoun, D., and A. G. Hawkes. 1982. On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 300:1–59. - PubMed
-
- Colquhoun, D., A. G. Hawkes, and K. Srodzinski. 1996. Joint distributions of apparent open and shut times of single-ion channels and maximum likelihood fitting of mechanisms. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 354:2555–2590.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

