How cellular movement determines the collective force generated by the Dictyostelium discoideum slug
- PMID: 15380385
- PMCID: PMC6457452
- DOI: 10.1016/j.jtbi.2004.06.015
How cellular movement determines the collective force generated by the Dictyostelium discoideum slug
Abstract
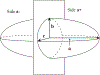
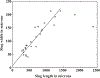
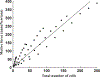
How the collective motion of cells in a biological tissue originates in the behavior of a collection of individuals, each of which responds to the chemical and mechanical signals it receives from neighbors, is still poorly understood. Here we study this question for a particular system, the slug stage of the cellular slime mold Dictyostelium discoideum (Dd). We investigate how cells in the interior of a migrating slug can effectively transmit stress to the substrate and thereby contribute to the overall motive force. Theoretical analysis suggests necessary conditions on the behavior of individual cells, and computational results shed light on experimental results concerning the total force exerted by a migrating slug. The model predicts that only cells in contact with the substrate contribute to the translational motion of the slug. Since the model is not based specifically on the mechanical properties of Dd cells, the results suggest that this behavior will be found in many developing systems.
Figures
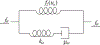

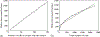
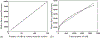
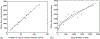
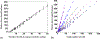


Similar articles
-
Viscoelastic cell model of sorting in the dictyostelium discoideum slug.PLoS One. 2025 May 28;20(5):e0325141. doi: 10.1371/journal.pone.0325141. eCollection 2025. PLoS One. 2025. PMID: 40435357 Free PMC article.
-
Cell sorting by differential cell motility: a model for pattern formation in Dictyostelium.J Theor Biol. 2004 Jan 21;226(2):215-24. doi: 10.1016/j.jtbi.2003.08.016. J Theor Biol. 2004. PMID: 14643191
-
Optical flow analysis of the ventral cellular layer of the migrating Dictyostelium discoideum slug.Microbiology (Reading). 1994 May;140 ( Pt 5):1241-52. doi: 10.1099/13500872-140-5-1241. Microbiology (Reading). 1994. PMID: 8025690
-
Cell size in Dictyostelium.Dev Genet. 1988;9(4-5):673-81. doi: 10.1002/dvg.1020090443. Dev Genet. 1988. PMID: 3072136 Review.
-
The extracellular matrix of the Dictyostelium discoideum slug.Experientia. 1995 Dec 18;51(12):1189-96. doi: 10.1007/BF01944736. Experientia. 1995. PMID: 8536806 Review.
Cited by
-
The anomalous diffusion of a tumor invading with different surrounding tissues.PLoS One. 2014 Oct 13;9(10):e109784. doi: 10.1371/journal.pone.0109784. eCollection 2014. PLoS One. 2014. PMID: 25310134 Free PMC article.
-
A model of fibroblast motility on substrates with different rigidities.Biophys J. 2010 Jun 16;98(12):2794-803. doi: 10.1016/j.bpj.2010.03.026. Biophys J. 2010. PMID: 20550891 Free PMC article.
-
Biophysical models of early mammalian embryogenesis.Stem Cell Reports. 2023 Jan 10;18(1):26-46. doi: 10.1016/j.stemcr.2022.11.021. Stem Cell Reports. 2023. PMID: 36630902 Free PMC article. Review.
-
Viscoelastic cell model of sorting in the dictyostelium discoideum slug.PLoS One. 2025 May 28;20(5):e0325141. doi: 10.1371/journal.pone.0325141. eCollection 2025. PLoS One. 2025. PMID: 40435357 Free PMC article.
-
Free and Interfacial Boundaries in Individual-Based Models of Multicellular Biological systems.Bull Math Biol. 2023 Oct 8;85(11):111. doi: 10.1007/s11538-023-01214-8. Bull Math Biol. 2023. PMID: 37805982 Free PMC article.
References
-
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P, 2002. Molecular Biology of the Cell, fourth ed. Garland, New York, London.
-
- Alt W, Dembo M, 1999. Cytoplasm dynamics and cell motion: two-phase flow models. Math. Biosci 156 (1), 207–228. - PubMed
-
- Beniot M, Gabriel D, Gerisch G, Gaub H, 2000. Discrete interactions in cell adhesion measured by single-molecule force spectroscopy. Nat. Cell Biol 2, 313–317. - PubMed
-
- Bonner JT, 1995. Why does slug length correlate with speed during migration in Dictyostelium discoideum?. J. Biosci 20 (1), 1–6.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

