The mechanics of surface expansion anisotropy in Medicago truncatula root hairs

Abstract

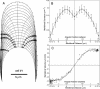
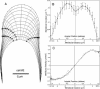
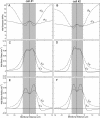
Wall expansion in tip-growing cells shows variations according to position and direction. In Medicago truncatula root hairs, wall expansion exhibits a strong meridional gradient with a maximum near the pole of the cell. Root hair cells also show a striking expansion anisotropy, i.e. over most of the dome surface the rate of circumferential wall expansion exceeds the rate of meridional expansion. Concomitant measurements of expansion rates and wall stresses reveal that the extensibility of the cell wall must vary abruptly along the meridian of the cell to maintain the gradient of wall expansion. To determine the mechanical basis of expansion anisotropy, we compared measurements of wall expansion with expansion patterns predicted from wall structural models that were either fully isotropic, transversely isotropic, or fully anisotropic. Our results indicate that a model based on a transversely isotropic wall structure can provide a good fit of the data although a fully anisotropic model offers the best fit overall. We discuss how such mechanical properties could be controlled at the microstructural level.

Figure 1.

A, Two alternatives for anisotropic wall expansion. In Nitella, stresses (solid arrows) favor transverse extension, but high mechanical anisotropy of the cell wall leads ultimately to axial extension. For tip-growing cells, we postulate that the cell wall has no intrinsic mechanical anisotropy in its plane so that expansion anisotropy reflects solely the bias in the wall stresses. B, Geometry of a tip-growing cell. The plane stresses (σ) acting on a small wall element are shown along with the strain rates () they produce.

Figure 2.

Raw data for cell number 1. A, Growth sequence of a M. truncatula root hair. The cell outline is shown at 3-min time intervals. The fiducial points used to define the cell geometry are highlighted on the last outline of the sequence. The position of surface markers (fluorescent microspheres) is also shown before (stars) and after (circles) projection onto the cell outlines. The axis of growth is the solid line following the pole of the cell through the entire sequence. Trajectories perpendicular to the cell outlines are indicated by dashed curves. B, Average κ_s for the cell. The observed mean and sd are shown at various locations. The solid line is the best fit of these data. C, Meridional velocity of surface markers shown in A. The solid line is the best fit of these data for n = 3 (see text).

Figure 3.

Raw data for cell number 2. Legend as for Figure 2.

Figure 4.

Meridional distribution of wall stresses and strain rates for two root hairs of M. truncatula. The left-hand and right-hand sections are for cell number 1 and cell number 2, respectively. A and B, Wall stresses inferred from the cell geometry. C and D, Strain rates derived from the best fit of the velocity data for n = 3. E and F, Predicted strain rates for a transversely isotropic cell wall. The shaded areas highlight the regions where the meridional stress exceeds the circumferential stress.

Figure 5.

Predicted cell wall extensibility for cell number 1 (solid line) and cell number 2 (dashed line).

Figure 6.

A, Models of cell wall structure showing the distribution of cellulose microfibrils within a wall element. For transversely isotropic and fully anisotropic models, cellulose microfibrils are confined to layers (s-θ planes) parallel to the cell surface. B, Anisotropy space. The stress and strain anisotropy for an isotropic material must lie on the line λ = 3γ (dotted line), while those for a transversely isotropic material must lie in the shaded area. The stress and strain anisotropy for a fully anisotropic material can occupy any point in the anisotropy space. The measured stress and strain anisotropy for cell number 1 and cell number 2 are shown (solid lines). The approximate meridional positions where the strain rates and stresses were measured are indicated. It can be seen that the data deviate from the region of transverse isotropy near to origin. The strain and stress anisotropy for the transversely isotropic model that best fit the data are shown (dashed lines). The strain and stress anisotropy observed in Nitella and Hydrodictyon (Green, 1963) are also included for comparison.