Spinal muscle forces, internal loads and stability in standing under various postures and loads--application of kinematics-based algorithm

Abstract

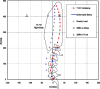
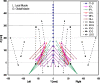
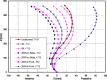
This work aimed to evaluate trunk muscle forces, internal loads and stability margin under some simulated standing postures, with and without external loads, using a nonlinear finite element model of the T1-S1 spine with realistic nonlinear load-displacement properties. A novel kinematics-based algorithm was applied that exploited a set of spinal sagittal rotations, initially calculated to minimize balancing moments, to solve the redundant active-passive system. The loads consisted of upper body gravity distributed along the spine with or without 200 N held in the hands, either in the front of the body or on the sides. Nonlinear and linear stability/perturbation analyses at deformed, stressed configurations with a linear stiffness-force relationship for muscles identified the system stability and critical muscle stiffness coefficient. Predictions were in good agreement with reported measurements of posture, muscle EMG and intradiscal pressure. Minimal changes in posture (posterior pelvic tilt and lumbar flattening) substantially influenced muscle forces, internal loads and stability margin. Addition of 200 N load in front of the body markedly increased the system stability, global muscle forces, and internal loads, which reached anterior shear and compression forces of approximately 500 N and approximately 1,200 N, respectively, at lower lumbar levels. Co-activation in abdominal muscles (up to 3% maximum force) substantially increased extensor muscle forces, internal loads and stability margin, allowing a smaller critical muscle coefficient. A tradeoff existed between lower internal loads in passive tissues and higher stability margins, as both increased with greater muscle activation. The strength of the proposed model is in accounting for the synergy by simultaneous consideration of passive structure and muscle forces under applied postures and loads.

Fig. 1

Sagittal profile of the model, T1–S1 consisting of seven rigid bodies and six deformable beam elements. The segmental stiffness is presented by deformable beam elements with nonlinear load-displacement properties in different directions at each T12–S1 disc level. The positions of distributed gravity load (total of 397.1 N) and concentrated 200 N load (held in front or on sides) are also shown. The rib cage and vertebral outlines are provided schematically for visualization (not to scale)

Fig. 2

Representation of global and local musculature in the coronal plane used in the T1–S1 model (IC iliocostalis, IP iliopsoas, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)

Fig. 3

Representation of global and local musculature in the sagittal plane used in the T1–S1 model (IC iliocostalis, IP iliopsoas, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)

Fig. 4

Optimal postures computed for the six cases (three load cases of gravity alone or with 200 N load held in front or on the sides for two optimization cases ± T12). These postures (pelvic tilt and sagittal rotations) are predicted by minimizing the sum of balancing moments at different levels