Ion permeation through the alpha-hemolysin channel: theoretical studies based on Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory

Abstract

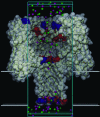
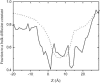
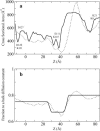
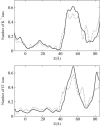
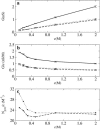
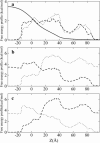
Identification of the molecular interaction governing ion conduction through biological pores is one of the most important goals of modern electrophysiology. Grand canonical Monte Carlo Brownian dynamics (GCMC/BD) and three-dimensional Poisson-Nernst-Plank (3d-PNP) electrodiffusion algorithms offer powerful and general approaches to study of ion permeation through wide molecular pores. A detailed analysis of ion flows through the staphylococcal alpha-hemolysin channel based on series of simulations at different concentrations and transmembrane potentials is presented. The position-dependent diffusion coefficient is approximated on the basis of a hydrodynamic model. The channel conductance calculated by GCMC/BD is approximately 10% higher than (electrophysiologically measured) experimental values, whereas results from 3d-PNP are always 30-50% larger. Both methods are able to capture all important electrostatic interactions in equilibrium conditions. The asymmetric conductance upon the polarity of the transmembrane potential observed experimentally is reproduced by GCMC/BD and 3d-PNP. The separation of geometrical and energetic influence of the channel on ion conduction reveals that such asymmetries arise from the permanent charge distribution inside the pore. The major determinant of the asymmetry is unbalanced charge in the triad of polar residues D127, D128, and K131. The GCMC/BD or 3d-PNP calculations reproduce also experimental reversal potentials and permeability rations in asymmetric ionic solutions. The weak anionic selectivity of the channel results from the presence of the salt bridge between E111 and K147 in the constriction zone. The calculations also reproduce the experimentally derived dependence of the reversible potential to the direction of the salt gradient. The origin of such effect arises from the asymmetrical distribution of energetic barriers along the channel axis, which modulates the preferential ion passage in different directions.

FIGURE 1

Molecular graphics view of the GCMC/BD simulation of the α-hemolysin pore bathed in 1.0 M KCl solution. Saggital section of the channel along the Z axis. The orthorhombic simulation box and the 3.0 Å regions corresponding to the buffer areas are drawn as cyan lines. The membrane is delimited by thick white lines. K⁺ (magenta) and Cl⁻ (green) ions are located in the pore and in the buffer regions.

FIGURE 2

Relative diffusion coefficient of Cl⁻ ion along OmpF channel axis from MD simulations (solid line) and hydrodynamic approximation (dotted line). The results for the K⁺ diffusion coefficient profile are similar and not shown here.

FIGURE 3

(a) Cross-sectional area of α-HL computed by a grid search (dotted line) and evaluated using a variable probe sphere moving along the channel axis (solid line). (b) Diffusion coefficient relative to a bulk value estimated by a hydrodynamic approximation (dots) and used in the BD and PNP computations (solid line). The center of the membrane is located at Z = 0.0. Å.

FIGURE 4

Average number of ions inside the channel pore along the Z axis from PB (dotted line) and BD (solid line). Three major regions can be distinguished: the wide and irregularly shaped extracellular vestibule (87–40 Å), the narrow constriction zone located at the stem neck (40–36 Å) and the long intracellular stem part of the channel (36 to −13.5 Å) formed by β-strands. The center of the membrane is located at Z = 0.0 Å.

FIGURE 5

Current-voltage relation in a 1.0 M KCl symmetric solution from GCMC/BD simulation and 3d-PNP computations. The total current (solid line) is the sum of K⁺ (dashed line) and Cl⁻ (dotted line) currents. Experimental data (▪) corresponding to the total current at V = 40mV and V = −40mV were taken from Menestrina (1986) and Miles et al. (2002), respectively.

FIGURE 6

(a) Conductance-concentration (G-c) relation (solid line) from GCMC/BD at V_mp = 150 mV with contribution from K⁺ (dashed line) and Cl⁻ (dotted line) currents. (b) Channel conductances normalized by a salt concentration. (c) Number of ions K⁺ (dashed line) and Cl⁻ (dotted line) inside the pore normalized by salt concentration from BD simulation without transmembrane potential.

FIGURE 7

(a) Effective one-dimensional free-energy profile of K⁺ (dashed line), Cl⁻ (dotted line), and the transmembrane potential (solid line) in a 1.0 M KCl symmetric solution. The center of the membrane is located at Z = 0.0 Å. The same profile combined with contribution from transmembrane potential of (b) +150mV and (c) −150mV.

FIGURE 8

Current-voltage relation in KCl asymmetric solution from GCMC/BD simulations. The total current (solid line) is the sum of K⁺ (dashed line) and Cl⁻ (dotted line) currents.

FIGURE 9

Current-voltage relation in KCl asymmetric solution from PNP computations. The total current (solid line) is the sum of K⁺ (dashed line) and Cl⁻ (dotted line) currents.