Hidden complexity of free energy surfaces for peptide (protein) folding
- PMID: 15466711
- PMCID: PMC522040
- DOI: 10.1073/pnas.0406234101
Hidden complexity of free energy surfaces for peptide (protein) folding
Abstract
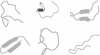
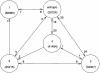
An understanding of the thermodynamics and kinetics of protein folding requires a knowledge of the free energy surface governing the motion of the polypeptide chain. Because of the many degrees of freedom involved, surfaces projected on only one or two progress variables are generally used in descriptions of the folding reaction. Such projections result in relatively smooth surfaces, but they could mask the complexity of the unprojected surface. Here we introduce an approach to determine the actual (unprojected) free energy surface and apply it to the second beta-hairpin of protein G, which has been used as a model system for protein folding. The surface is represented by a disconnectivity graph calculated from a long equilibrium folding-unfolding trajectory. The denatured state is found to have multiple low free energy basins. Nevertheless, the peptide shows exponential kinetics in folding to the native basin. Projected surfaces obtained from the present analysis have a simple form in agreement with other studies of the beta-hairpin. The hidden complexity found for the beta-hairpin surface suggests that the standard funnel picture of protein folding should be revisited.
Figures
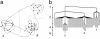

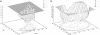
References
-
- Becker, O. M. & Karplus, M. (1997) J. Chem. Phys. 106, 1495–1517.
-
- Wales, D. J., Miller, M. A. & Walsh, T. R. (1998) Nature 394, 758–760.
-
- Levy, Y. & Becker, O. M. (1998) Phys. Rev. Lett. 81, 1126–1129.
-
- Krivov, S. V. & Karplus, M. (2002) J. Chem. Phys. 117, 10894–10903.
-
- Wales, D. J. (2003) Energy Landscapes (Cambridge Univ. Press, Cambridge, U.K.).
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

