Three-body interactions improve the prediction of rate and mechanism in protein folding models

Abstract

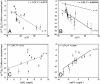
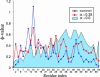
Here we study the effects of many-body interactions on rate and mechanism in protein folding by using the results of molecular dynamics simulations on numerous coarse-grained Calpha-model single-domain proteins. After adding three-body interactions explicitly as a perturbation to a Gō-like Hamiltonian with native pairwise interactions only, we have found (i) a significantly increased correlation with experimental phi values and folding rates, (ii) a stronger correlation of folding rate with contact order, matching the experimental range in rates when the fraction of three-body energy in the native state is approximately 20%, and (iii) a considerably larger amount of three-body energy present in chymotripsin inhibitor than in the other proteins studied.

Fig. 1.

The folding barrier height ΔF^≠ increases with increasing three-body contribution to the energy α. (A) Free energy versus the fraction of native contacts Q for CI2 for three values of α.(B) The barrier versus α for four proteins selected from Table 1. Shown for CI2 are error bars obtained from the standard deviation of F(Q) by using a bin size ΔQ = 4/149. (C) The average slope of ΔF^≠versus α correlates strongly with the number of three-body interactions in the native state (r = 0.89, P = 10^–6). Therefore, the barriers in B increase at different rates because of differing numbers of triples formed in the transition states of the various proteins: More native triples typically means a larger three-body contribution to the barrier. The shaded region in A corresponds to the TTSE described in Materials and Methods. In general, this ensemble depends on α.

Fig. 2.

Comparison of simulated and experimental rates. (A) Simulated folding barriers (effectively measuring logarithm folding rates for 18 proteins listed in Materials and Methods) for a pairwise interacting Gō model correlate well with absolute contact order (aCO) (43). (B) Simulated folding barriers show an increased correlation with absolute contact order when the fraction of native three-body energy is such that the dispersion in effective simulated rates matches the experimental dispersion for this dataset (α = 20%). Rates now span 5.7 decades, in contrast to 2 decades for a pure two-body Hamiltonian (dashed line in B is the best fit line in A). (C) For 13 of the 18 proteins (see Materials and Methods for a list), rate data were available for various different denaturant concentrations. These proteins were used for the analysis in C and D. For these proteins, the simulated effective log rates do not correlate significantly with the experimental rate data at 25°C. (D) By tuning the rate data to the transition midpoints and introducing three-body energy in the native state, we saw a significant increase in the correlation between experimental and simulated rate data, with best correlation when α = 10%.

Fig. 3.

Comparison of the agreement of φ values between simulation and experiment for CI2 (A) and SH3 (B). Green curves show the correlation coefficient and statistical significance (Insets) for φ values derived from the TTSE in the simulations as the Hamiltonian was continuously changed from a uniform Gō model to one with pair interactions governed by MJ parameters (the curve shown in A Inset is the statistical significance of the anticorrelation) (see Eq. 6). No improvement was seen for CI2 or SH3 by implementing this recipe. Red and blue curves show the correlation coefficient and statistical significance between experimental and simulated φ values as a function of the fraction α of three-body energy in the native state. Blue curves correspond to TTSE; red curves correspond to KTSE. For CI2, the improvement as α is increased is dramatic, with best agreement with the experiment at ≈35% three-body energy. On the other hand, SH3 was exceptional in that it showed the opposite trend, with best agreement for a purely pairwise interacting model for the TTSE and α = 5% for the KTSE. All other proteins studied were bracketed by these two extremes: They showed moderate components of three-body energy, with moderate to large increases in correlation coefficient (Table 1).

Fig. 4.

Plot of the largest improvement in correlation (r_α*^–r_o) vs. the value of interpolation parameter α* required to achieve that correlation. Energy functions are interpolated toward a three-body Gō model (Eq. 1) and two-body models with MJ energetic parameters (Eq. 6). The slope and correlation indicate the validity of the interpolation procedure. Adding three-body energies gives a slope of 2.2, and (r = 0.97 and P = 0.005). Adding a MJ component to the pair interaction energies gives a slope of 0.29 but a fit that is not statistically significant (r = 0.83 and P = 0.38). Restricting the MJ component to native interaction energies gives a statistically significant fit (r = 0.956 and P = 0.044) but with a shallow slope (0.78), indicating only moderate improvement.

Fig. 5.

φ value versus residue index for CI2, for experiment (blue trace), simulated pairwise Gō model (light-blue background), and two- plus three-body Gō model (red trace). The average φ values for the various energy functions are , , , again confirming the more accurate two-plus three-body transition state is less structured. It is worth noting that native state is more stable in the experiments than in the simulations: The native stability is fixed at the transition midpoint in the simulations, regardless of the value of α.