FPL 64176 modification of Ca(V)1.2 L-type calcium channels: dissociation of effects on ionic current and gating current
- PMID: 15501945
- PMCID: PMC1304999
- DOI: 10.1529/biophysj.104.051714
FPL 64176 modification of Ca(V)1.2 L-type calcium channels: dissociation of effects on ionic current and gating current
Abstract
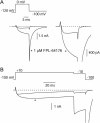
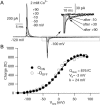
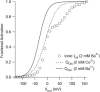
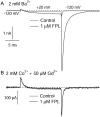
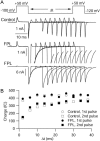
FPL 64176 (FPL) is a nondihydropyridine compound that dramatically increases macroscopic inward current through L-type calcium channels and slows activation and deactivation. To understand the mechanism by which channel behavior is altered, we compared the effects of the drug on the kinetics and voltage dependence of ionic currents and gating currents. Currents from a homogeneous population of channels were obtained using cloned rabbit Ca(V)1.2 (alpha1C, cardiac L-type) channels stably expressed in baby hamster kidney cells together with beta1a and alpha2delta1 subunits. We found a striking dissociation between effects of FPL on ionic currents, which were modified strongly, and on gating currents, which were not detectably altered. Inward ionic currents were enhanced approximately 5-fold for a voltage step from -90 mV to +10 mV. Kinetics of activation and deactivation were slowed dramatically at most voltages. Curiously, however, at very hyperpolarized voltages (< -250 mV), deactivation was actually faster in FPL than in control. Gating currents were measured using a variety of inorganic ions to block ionic current and also without blockers, by recording gating current at the reversal potential for ionic current (+50 mV). Despite the slowed kinetics of ionic currents, FPL had no discernible effect on the fundamental movements of gating charge that drive channel gating. Instead, FPL somehow affects the coupling of charge movement to opening and closing of the pore. An intriguing possibility is that the drug causes an inactivated state to become conducting without otherwise affecting gating transitions.
Figures




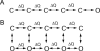


Similar articles
-
Kinetic effects of FPL 64176 on L-type Ca2+ channels in cardiac myocytes.Naunyn Schmiedebergs Arch Pharmacol. 2000 May;361(5):465-76. doi: 10.1007/s002100000219. Naunyn Schmiedebergs Arch Pharmacol. 2000. PMID: 10832599
-
Modulation of single channels underlying hippocampal L-type current enhancement by agonists depends on the permeant ion.J Neurophysiol. 2004 Aug;92(2):824-37. doi: 10.1152/jn.00700.2003. Epub 2004 Mar 31. J Neurophysiol. 2004. PMID: 15056682
-
Biophysical and pharmacological characterization of voltage-gated calcium currents in turtle auditory hair cells.J Physiol. 2003 Jun 15;549(Pt 3):697-717. doi: 10.1113/jphysiol.2002.037481. Epub 2003 May 9. J Physiol. 2003. PMID: 12740421 Free PMC article.
-
Direct Estimation of CaV1.2 Gating Parameters: Quantification of Voltage Sensor - Pore Transductions and their Modulation by FLP 64176.Curr Mol Pharmacol. 2015;8(1):87-94. doi: 10.2174/1874467208666150507100256. Curr Mol Pharmacol. 2015. PMID: 25966699 Review.
-
Metal ion effects on ion channel gating.Q Rev Biophys. 2003 Nov;36(4):373-427. doi: 10.1017/s0033583504003932. Q Rev Biophys. 2003. PMID: 15267168 Review.
Cited by
-
IGFBPL1 Regulates Axon Growth through IGF-1-mediated Signaling Cascades.Sci Rep. 2018 Feb 1;8(1):2054. doi: 10.1038/s41598-018-20463-5. Sci Rep. 2018. PMID: 29391597 Free PMC article.
-
Calcium signals that determine vascular resistance.Wiley Interdiscip Rev Syst Biol Med. 2019 Sep;11(5):e1448. doi: 10.1002/wsbm.1448. Epub 2019 Mar 18. Wiley Interdiscip Rev Syst Biol Med. 2019. PMID: 30884210 Free PMC article. Review.
-
Loss of Ca(v)1.3 (CACNA1D) function in a human channelopathy with bradycardia and congenital deafness.Nat Neurosci. 2011 Jan;14(1):77-84. doi: 10.1038/nn.2694. Epub 2010 Dec 5. Nat Neurosci. 2011. PMID: 21131953
-
Characterization of Na+ and Ca2+ channels in zebrafish dorsal root ganglion neurons.PLoS One. 2012;7(8):e42602. doi: 10.1371/journal.pone.0042602. Epub 2012 Aug 3. PLoS One. 2012. PMID: 22880050 Free PMC article.
-
Open-state occupancy prevents gating charge relaxation of N-type (CaV2.2) calcium channels.Biophys J. 2009 Nov 4;97(9):2446-55. doi: 10.1016/j.bpj.2009.08.014. Biophys J. 2009. PMID: 19883587 Free PMC article.
References
-
- Altier, C., R. L. Spaetgens, J. Nargeot, E. Bourinet, and G. W. Zamponi. 2001. Multiple structural elements contribute to voltage-dependent facilitation of neuronal α1C (CaV1.2) L-type calcium channels. Neuropharmacology. 40:1050–1057. - PubMed
-
- Artigas, P., G. Ferreira, N. Reyes, G. Brum, and G. Pizarro. 2003. Effects of the enantiomers of BayK 8644 on the charge movement of L-type Ca channels in guinea-pig ventricular myocytes. J. Membr. Biol. 193:215–227. - PubMed
-
- Baxter, A. J. G., J. Dixon, F. Ince, C. N. Manners, and S. J. Teague. 1993. Discovery and synthesis of methyl 2,5-dimethyl-4-[2-(phenylmethyl)benzoyl]-1H-pyrrole-3-carboxylate (FPL 64176) and analogues: the first examples of a new class of calcium channel activator. J. Med. Chem. 36:2739–2744. - PubMed
-
- Bean, B. P. 1993. Beta-adrenergic modulation of cardiac Ca channel gating. In Ion Channels in the Cardiovascular System: Function and Dysfunction. A. M. Brown, W. A. Catterall, P. M. Spooner, and H. C. Strauss, editors. Futura Press, Armonk, NY. 237–252.
-
- Bean, B. P., M. C. Nowycky, and R. W. Tsien. 1984. Beta-adrenergic modulation of calcium channels in frog ventricular heart cells. Nature. 307:371–375. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

