An information integration theory of consciousness
- PMID: 15522121
- PMCID: PMC543470
- DOI: 10.1186/1471-2202-5-42
An information integration theory of consciousness
Abstract
Background: Consciousness poses two main problems. The first is understanding the conditions that determine to what extent a system has conscious experience. For instance, why is our consciousness generated by certain parts of our brain, such as the thalamocortical system, and not by other parts, such as the cerebellum? And why are we conscious during wakefulness and much less so during dreamless sleep? The second problem is understanding the conditions that determine what kind of consciousness a system has. For example, why do specific parts of the brain contribute specific qualities to our conscious experience, such as vision and audition?
Presentation of the hypothesis: This paper presents a theory about what consciousness is and how it can be measured. According to the theory, consciousness corresponds to the capacity of a system to integrate information. This claim is motivated by two key phenomenological properties of consciousness: differentiation - the availability of a very large number of conscious experiences; and integration - the unity of each such experience. The theory states that the quantity of consciousness available to a system can be measured as the Phi value of a complex of elements. Phi is the amount of causally effective information that can be integrated across the informational weakest link of a subset of elements. A complex is a subset of elements with Phi>0 that is not part of a subset of higher Phi. The theory also claims that the quality of consciousness is determined by the informational relationships among the elements of a complex, which are specified by the values of effective information among them. Finally, each particular conscious experience is specified by the value, at any given time, of the variables mediating informational interactions among the elements of a complex.
Testing the hypothesis: The information integration theory accounts, in a principled manner, for several neurobiological observations concerning consciousness. As shown here, these include the association of consciousness with certain neural systems rather than with others; the fact that neural processes underlying consciousness can influence or be influenced by neural processes that remain unconscious; the reduction of consciousness during dreamless sleep and generalized seizures; and the time requirements on neural interactions that support consciousness.
Implications of the hypothesis: The theory entails that consciousness is a fundamental quantity, that it is graded, that it is present in infants and animals, and that it should be possible to build conscious artifacts.
Figures
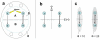
 B) = EI(A→B) + EI(B→A). b. Minimum information bipartition. For subset S = {1,2,3,4}, the horizontal bipartition {1,3}/{2,4} yields a positive value of EI. However, the bipartition {1,2}/{3,4} yields EI = 0 and is a minimum information bipartition (MIB) for this subset. The other bipartitions of subset S = {1,2,3,4} are {1,4}/{2,3}, {1}/{2,3,4}, {2}/{1,3,4}, {3}/{1,2,4}, {4}/{1,2,3}, all with EI>0. c. Analysis of complexes. By considering all subsets of system X one can identify its complexes and rank them by the respective values of Φ – the value of EI for their minimum information bipartition. Assuming that other elements in X are disconnected, it is easy to see that Φ>0 for subset {3,4} and {1,2}, but Φ = 0 for subsets {1,3}, {1,4}, {2,3}, {2,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, and {1,2,3,4}. Subsets {3,4} and {1,2} are not part of a larger subset having higher Φ, and therefore they constitute complexes. This is indicated schematically by having them encircled by a grey oval (darker grey indicates higher Φ). Methodological note. In order to identify complexes and their Φ(S) for systems with many different connection patterns, each system X was implemented as a stationary multidimensional Gaussian process such that values for effective information could be obtained analytically (details in [8]). Briefly, in order to identify complexes and their Φ(S) for systems with many different connection patterns, we implemented numerous model systems X composed of n neural elements with connections CONij specified by a connection matrix CON(X) (no self-connections). In order to compare different architectures, CON(X) was normalized so that the absolute value of the sum of the afferent synaptic weights per element corresponded to a constant value w<1 (here w = 0.5). If the system's dynamics corresponds to a multivariate Gaussian random process, its covariance matrix COV(X) can be derived analytically. As in previous work, we consider the vector X of random variables that represents the activity of the elements of X, subject to independent Gaussian noise R of magnitude c. We have that, when the elements settle under stationary conditions, X = X * CON(X) + cR. By defining Q = (1-CON(X))-1 and averaging over the states produced by successive values of R, we obtain the covariance matrix COV(X) = <X*X> = <Qt * Rt * R * Q> = Qt * Q, where the superscript t refers to the transpose. Under Gaussian assumptions, all deviations from independence among the two complementary parts A and B of a subset S of X are expressed by the covariances among the respective elements. Given these covariances, values for the individual entropies H(A) and H(B), as well as for the joint entropy of the subset H(S) = H(AB) can be obtained as, for example, H(A) = (1/2)ln [(2π e)n|COV(A)|], where |•| denotes the determinant. The mutual information between A and B is then given by MI(A;B) = H(A) + H(B) - H(AB). Note that MI(A:B) is symmetric and positive. To obtain the effective information between A and B within model systems, independent noise sources in A are enforced by setting to zero strength the connections within A and afferent to A. Then the covariance matrix for A is equal to the identity matrix (given independent Gaussian noise), and any statistical dependence between A and B must be due to the causal effects of A on B, mediated by the efferent connections of A. Moreover, all possible outputs from A that could affect B are evaluated. Under these conditions, EI(A→B) = MI(AHmax;B). The independent Gaussian noise R applied to A is multiplied by cp, the perturbation coefficient, while the independent Gaussian noise applied to the rest of the system is given by ci, the intrinsic noise coefficient. Here cp = 1 and ci = 0.00001 in order to emphasize the role of the connectivity and minimize that of noise. To identify complexes and obtain their capacity for information integration, one considers every subset S of X composed of k elements, with k = 2,..., n. For each subset S, we consider all bipartitions and calculate EI(A
B) = EI(A→B) + EI(B→A). b. Minimum information bipartition. For subset S = {1,2,3,4}, the horizontal bipartition {1,3}/{2,4} yields a positive value of EI. However, the bipartition {1,2}/{3,4} yields EI = 0 and is a minimum information bipartition (MIB) for this subset. The other bipartitions of subset S = {1,2,3,4} are {1,4}/{2,3}, {1}/{2,3,4}, {2}/{1,3,4}, {3}/{1,2,4}, {4}/{1,2,3}, all with EI>0. c. Analysis of complexes. By considering all subsets of system X one can identify its complexes and rank them by the respective values of Φ – the value of EI for their minimum information bipartition. Assuming that other elements in X are disconnected, it is easy to see that Φ>0 for subset {3,4} and {1,2}, but Φ = 0 for subsets {1,3}, {1,4}, {2,3}, {2,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, and {1,2,3,4}. Subsets {3,4} and {1,2} are not part of a larger subset having higher Φ, and therefore they constitute complexes. This is indicated schematically by having them encircled by a grey oval (darker grey indicates higher Φ). Methodological note. In order to identify complexes and their Φ(S) for systems with many different connection patterns, each system X was implemented as a stationary multidimensional Gaussian process such that values for effective information could be obtained analytically (details in [8]). Briefly, in order to identify complexes and their Φ(S) for systems with many different connection patterns, we implemented numerous model systems X composed of n neural elements with connections CONij specified by a connection matrix CON(X) (no self-connections). In order to compare different architectures, CON(X) was normalized so that the absolute value of the sum of the afferent synaptic weights per element corresponded to a constant value w<1 (here w = 0.5). If the system's dynamics corresponds to a multivariate Gaussian random process, its covariance matrix COV(X) can be derived analytically. As in previous work, we consider the vector X of random variables that represents the activity of the elements of X, subject to independent Gaussian noise R of magnitude c. We have that, when the elements settle under stationary conditions, X = X * CON(X) + cR. By defining Q = (1-CON(X))-1 and averaging over the states produced by successive values of R, we obtain the covariance matrix COV(X) = <X*X> = <Qt * Rt * R * Q> = Qt * Q, where the superscript t refers to the transpose. Under Gaussian assumptions, all deviations from independence among the two complementary parts A and B of a subset S of X are expressed by the covariances among the respective elements. Given these covariances, values for the individual entropies H(A) and H(B), as well as for the joint entropy of the subset H(S) = H(AB) can be obtained as, for example, H(A) = (1/2)ln [(2π e)n|COV(A)|], where |•| denotes the determinant. The mutual information between A and B is then given by MI(A;B) = H(A) + H(B) - H(AB). Note that MI(A:B) is symmetric and positive. To obtain the effective information between A and B within model systems, independent noise sources in A are enforced by setting to zero strength the connections within A and afferent to A. Then the covariance matrix for A is equal to the identity matrix (given independent Gaussian noise), and any statistical dependence between A and B must be due to the causal effects of A on B, mediated by the efferent connections of A. Moreover, all possible outputs from A that could affect B are evaluated. Under these conditions, EI(A→B) = MI(AHmax;B). The independent Gaussian noise R applied to A is multiplied by cp, the perturbation coefficient, while the independent Gaussian noise applied to the rest of the system is given by ci, the intrinsic noise coefficient. Here cp = 1 and ci = 0.00001 in order to emphasize the role of the connectivity and minimize that of noise. To identify complexes and obtain their capacity for information integration, one considers every subset S of X composed of k elements, with k = 2,..., n. For each subset S, we consider all bipartitions and calculate EI(A  B) for each of them. We find the minimum information bipartition MIB(S), the bipartition for which the normalized effective information reaches a minimum, and the corresponding value of Φ(S). We then find the complexes of X as those subsets S with Φ>0 that are not included within a subset having higher Φ and rank them based on their Φ(S) value. The complex with the maximum value of Φ(S) is the main complex. MATLAB functions used for calculating effective information and complexes are at
B) for each of them. We find the minimum information bipartition MIB(S), the bipartition for which the normalized effective information reaches a minimum, and the corresponding value of Φ(S). We then find the complexes of X as those subsets S with Φ>0 that are not included within a subset having higher Φ and rank them based on their Φ(S) value. The complex with the maximum value of Φ(S) is the main complex. MATLAB functions used for calculating effective information and complexes are at 

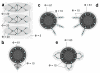

References
-
- Tononi G. Information measures for conscious experience. Arch Ital Biol. 2001;139:367–371. - PubMed
-
- Tononi G. Consciousness and the brain: Theoretical aspects. In: Adelman G, Smith, B, editor. Encyclopedia of Neuroscience. 3. Elsevier; 2004.
-
- Shannon CE, Weaver W. The mathematical theory of communication. Urbana: University of Illinois Press; 1963.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

