Mechanics of transient platelet adhesion to von Willebrand factor under flow
- PMID: 15533923
- PMCID: PMC1305145
- DOI: 10.1529/biophysj.104.047001
Mechanics of transient platelet adhesion to von Willebrand factor under flow
Abstract
A primary and critical step in platelet attachment to injured vascular endothelium is the formation of reversible tether bonds between the platelet glycoprotein receptor Ibalpha and the A1 domain of surface-bound von Willebrand factor (vWF). Due to the platelet's unique ellipsoidal shape, the force mechanics involved in its tether bond formation differs significantly from that of leukocytes and other spherical cells. We have investigated the mechanics of platelet tethering to surface-immobilized vWF-A1 under hydrodynamic shear flow. A computer algorithm was used to analyze digitized images recorded during flow-chamber experiments and track the microscale motions of platelets before, during, and after contact with the surface. An analytical two-dimensional model was developed to calculate the motion of a tethered platelet on a reactive surface in linear shear flow. Through comparison of the theoretical solution with experimental observations, we show that attachment of platelets occurs only in orientations that are predicted to result in compression along the length of the platelet and therefore on the bond being formed. These results suggest that hydrodynamic compressive forces may play an important role in initiating tether bond formation.
Figures
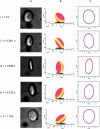

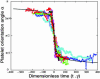
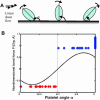
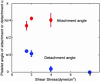
Similar articles
-
Shear stress-induced binding of large and unusually large von Willebrand factor to human platelet glycoprotein Ibalpha.Ann Biomed Eng. 2004 Jul;32(7):961-9. doi: 10.1023/b:abme.0000032458.88212.54. Ann Biomed Eng. 2004. PMID: 15298433
-
The N-terminal flanking region of the A1 domain regulates the force-dependent binding of von Willebrand factor to platelet glycoprotein Ibα.J Biol Chem. 2013 Nov 8;288(45):32289-32301. doi: 10.1074/jbc.M113.504001. Epub 2013 Sep 23. J Biol Chem. 2013. PMID: 24062306 Free PMC article. Clinical Trial.
-
Shear-dependent rolling on von Willebrand factor of mammalian cells expressing the platelet glycoprotein Ib-IX-V complex.Blood. 1998 Nov 15;92(10):3684-93. Blood. 1998. PMID: 9808562
-
Platelet-vessel wall interactions in thrombosis and restenosis role of von Willebrand factor.Verh K Acad Geneeskd Belg. 1997;59(3):161-83. Verh K Acad Geneeskd Belg. 1997. PMID: 9490916 Review.
-
Thrombus Formation at High Shear Rates.Annu Rev Biomed Eng. 2017 Jun 21;19:415-433. doi: 10.1146/annurev-bioeng-071516-044539. Epub 2017 Apr 24. Annu Rev Biomed Eng. 2017. PMID: 28441034 Review.
Cited by
-
Simulation of platelet, thrombus and erythrocyte hydrodynamic interactions in a 3D arteriole with in vivo comparison.PLoS One. 2013 Oct 2;8(10):e76949. doi: 10.1371/journal.pone.0076949. eCollection 2013. PLoS One. 2013. PMID: 24098571 Free PMC article.
-
Platelet adhesive dynamics. Part I: characterization of platelet hydrodynamic collisions and wall effects.Biophys J. 2008 Sep;95(5):2539-55. doi: 10.1529/biophysj.107.127670. Epub 2008 May 30. Biophys J. 2008. PMID: 18515387 Free PMC article.
-
DNA modification of live cell surface.Nucleic Acids Res. 2009 Mar;37(4):e28. doi: 10.1093/nar/gkn1034. Epub 2009 Jan 21. Nucleic Acids Res. 2009. PMID: 19158188 Free PMC article.
-
Binary agonist surface patterns prime platelets for downstream adhesion in flowing whole blood.Biointerphases. 2017 Apr 28;12(2):02C406. doi: 10.1116/1.4982596. Biointerphases. 2017. PMID: 28454486 Free PMC article.
-
The Effect of Hematocrit on Platelet Adhesion: Experiments and Simulations.Biophys J. 2016 Aug 9;111(3):577-588. doi: 10.1016/j.bpj.2016.06.024. Biophys J. 2016. PMID: 27508441 Free PMC article.
References
-
- Alevriadou, B. R., J. L. Moake, N. A. Turner, Z. M. Ruggeri, B. J. Folie, M. D. Phillips, A. B. Schreiber, M. E. Hrinda, and L. V. McIntire. 1993. Real-time analysis of shear-dependent thrombus formation and its blockade by inhibitors of von Willebrand factor binding to platelets. Blood. 81:1263–1276. - PubMed
-
- Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. - PubMed
-
- Batchelor, G. K., and J. T. Green. 1972. The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56:375–400.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

