Membrane-protein interactions in mechanosensitive channels
- PMID: 15542561
- PMCID: PMC1305162
- DOI: 10.1529/biophysj.104.047431
Membrane-protein interactions in mechanosensitive channels
Abstract
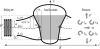
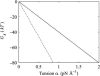
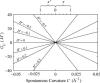
In this article, we examine the mechanical role of the lipid bilayer in ion channel conformation and function with specific reference to the case of the mechanosensitive channel of large conductance (MscL). In a recent article we argued that mechanotransduction very naturally arises from lipid-protein interactions by invoking a simple analytic model of the MscL channel and the surrounding lipid bilayer. In this article, we focus on improving and expanding this analytic framework for studying lipid-protein interactions with special attention to MscL. Our goal is to generate simple scaling relations which can be used to provide qualitative understanding of the role of membrane mechanics in protein function and to quantitatively interpret experimental results. For the MscL channel, we find that the free energies induced by lipid-protein interaction are of the same order as the measured free energy differences between conductance states. We therefore conclude that the mechanics of the bilayer plays an essential role in determining the conformation and function of the channel. Finally, we compare the predictions of our model to experimental results from the recent investigations of the MscL channel by a variety of investigators and suggest a suite of new experiments.
Figures


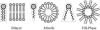










References
-
- Bass, R. B., P. Srop, M. Barclay, and D. C. Rees. 2002. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 298:1582–1587. - PubMed
-
- Betanzos, M., C. S. Chiang, H. R. Guy, and S. Sukharev. 2002. A large iris-like expansion of a mechanosensitive channel protein induced by membrane tension. Nat. Struct. Biol. 9:704–710. - PubMed
-
- Bilston, L. E., and K. Mylvaganam. 2002. Molecular simulations of the large conductance mechanosensitive (MscL) channel under mechanical loading. FEBS Lett. 512:185–190. - PubMed
-
- Blount, P., and P. C. Moe. 1999. Bacterial mechanosensitive channels: integrating physiology, structure and function. Trends Microbiol. 7:420–424. - PubMed
-
- Boal, D. 2002. Mechanics of the Cell. Cambridge University Press, Cambridge, UK.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

