Recycling Frank: Spontaneous emergence of homochirality in noncatalytic systems

Abstract

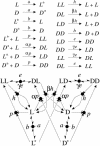
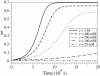
In this work, we introduce a prebiotically relevant protometabolic pattern corresponding to an engine of deracemization by using an external energy source. The spontaneous formation of a nonracemic mixture of chiral compounds can be observed in out-of-equilibrium systems via a symmetry-breaking phenomenon. This observation is possible thanks to chirally selective autocatalytic reactions (Frank's model) [Frank, F. C. (1953) Biochim. Biophys. Acta 11, 459-463]. We show that the use of a Frank-like model in a recycled system composed of reversible chemical reactions, rather than the classical irreversible system, allows for the emergence of a synergetic autoinduction from simple reactions, without any autocatalytic or even catalytic reaction. This model is described as a theoretical framework, based on the stereoselective reactivity of preexisting chiral monomeric building blocks (polymerization, epimerization, and depolymerization) maintained out of equilibrium by a continuous energy income, via an activation reaction. It permits the self-conversion of all monomeric subunits into a single chiral configuration. Real prebiotic systems of amino acid derivatives can be described on this basis. They are shown to be able to spontaneously reach a stable nonracemic state in a few centuries. In such systems, the presence of epimerization reactions is no more destructive, but in contrast is the central driving force of the unstabilization of the racemic state.

Fig. 1.

Minimal APED system limited to dimerizations of L and D residues. (Upper) Chemical reactions. (Lower) Reaction network. a, Activation; b, deactivation; p, homochiral polymerization; αp, heterochiral polymerization; h, homochiral hydrolysis; βh, heterochiral hydrolysis; e, homochiral epimerization; γe, heterochiral epimerization.

Fig. 2.

Schematic representations of Frank's model (A) and the APED model (B). (A) Circled S, synthesis of chiral compounds X_L and X_D from achiral compounds F; circled C, autocatalysis by X_L and X_D; circled M, mutual destruction of X_L and X_D to P. (B) Circled A, activation of L and D to L* and D*; circled P, polymerization from L* and D* to X_n; circled E, epimerization between polymers; circled D, depolymerization of X_n back to L and D.

Fig. 3.

The five kinds of behaviors of APED systems. (A–E) Spontaneous evolution of the enantiomeric excess of several simplified APED systems, calculated for b = 0 s^–1, a = h = e = 1 s^–1, p = 1 s^–1·M^–1, β = γ = 0 and α =0.1, c = 1M(A); α = 0.1, c = 3M(B); α = 1.1, c = 3.2M(C); α = 50, c = 2M(D); and α = 100, c = 2M(E). (F) Behavior categories of the simplified APED systems. Crosses indicate the position of the A–E system. Solid lines indicate the separations between dead (d), symmetric (s), asymmetric (a), and unstable (u) systems. The dotted line represents the separation between monotone and oscillating symmetric systems.

Fig. 4.

Diagram of the APED states as a function of α, β, and γ, calculated for b = 0 s^–1, a = h = e = 1 s^–1, p = 1 s^–1·M^–1, and c = 1M. a: Asymmetric system; s: symmetric system; d: dead system; u: unstable system. (A) Complete αβγ diagram. The dotted axes represents the values of α, β, and γ on a logarithmic scales, from 10^–4 to 10^1.5, and intersect at α = β = γ = 1. (B) βγ Diagram for α = 10^–1 (bilogarithmic scale). (C) αγ Diagram for β = 10^–2 (bilogarithmic scale). (D) Bifurcation diagram for α = 10^–1, representing the enantiomeric excess of the stable fixed point (|ee^fixe|) as a function of β = γ (logarithmic scale). (E) Bifurcation diagram for β = γ = 10^–2, representing |ee^fixe| as a function of α (logarithmic scale).

Fig. 5.

Time evolution of the enantiomeric excess of APED systems based on experimental data, for different concentrations in residues c. Calculated for eeⁱⁿⁱ = 0.01; a = 10^–8 s^–1, b = 5·10^–4 s^–1, p = 2·10^·2 s^–1·M^–1, α = 0.35, h = 10^–7 s^–1, β = 0.2, e = 10^–7 s^–1, γ = 0.3.