Evolution of dominance in metabolic pathways

Abstract

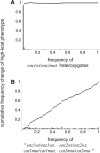
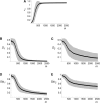
Dominance is a form of phenotypic robustness to mutations. Understanding how such robustness can evolve provides a window into how the relation between genotype and phenotype can evolve. As such, the issue of dominance evolution is a question about the evolution of inheritance systems. Attempts at explaining the evolution of dominance have run into two problems. One is that selection for dominance is sensitive to the frequency of heterozygotes. Accordingly, dominance cannot evolve unless special conditions lead to the presence of a high frequency of mutant alleles in the population. Second, on the basis of theoretical results in metabolic control analysis, it has been proposed that metabolic systems possess inherent constraints. These hypothetical constraints imply the default manifestation of dominance of the wild type with respect to the effects of mutations at most loci. Hence, some biologists have maintained that an evolutionary explanation is not relevant to dominance. In this article, we put into question the hypothetical assumption of default metabolic constraints. We show that this assumption is based on an exclusion of important nonlinear interactions that can occur between enzymes in a pathway. With an a priori exclusion of such interactions, the possibility of epistasis and hence dominance modification is eliminated. We present a theoretical model that integrates enzyme kinetics and population genetics to address dominance evolution in metabolic pathways. In the case of mutations that decrease enzyme concentrations, and given the mechanistic constraints of Michaelis-Menten-type catalysis, it is shown that dominance of the wild type can be extensively modified in a two-enzyme pathway. Moreover, we discuss analytical results indicating that the conclusions from the two-enzyme case can be generalized to any number of enzymes. Dominance modification is achieved chiefly through changes in enzyme concentrations or kinetic parameters such as k(cat), both of which can alter saturation levels. Low saturation translates into higher levels of dominance with respect to mutations that decrease enzyme concentrations. Furthermore, it is shown that in the two-enzyme example, dominance evolves as a by-product of selection in a manner that is insensitive to the frequency of heterozygotes. Using variation in k(cat) as an example of modifier mutations, it is shown that the latter can have direct fitness effects in addition to dominance modification effects. Dominance evolution can occur in a frequency-insensitive manner as a result of selection for such dual-effects alleles. This type of selection may prove to be a common pattern for the evolution of phenotypic robustness to mutations.

Figure 1.—

Cumulative frequency distribution of ∂_αiJ/J values for enzymes 1 and 2. Positive values for ∂_αi J indicate that flux increases when a mutation increases the k_cati of a given enzyme i.

Figure 2.—

Distributions of the effects of k_cat1 mutations on robustness properties of enzyme 1. The four quadrants represent different kinetic regimes. A positive λ_i value indicates a tendency toward increased sensitivity. A negative λ_i value indicates increased robustness.

Figure 3.—

Distributions of the effects of k_cat2 mutations on robustness properties of enzyme 2. The four quadrants represent different kinetic regimes. A positive λ_i value indicates a tendency toward increased sensitivity. A negative λ_i value indicates increased robustness.

Figure 4.—

Effects of finite changes in k_cat1 on flux J in an exergonic pathway. Point A lies in a region where Sat₁ > Sat₂. A mutation from A* to A leads to increased sensitivity to δE₁. Point B lies in a region where Sat₁ < Sat₂. A mutation from B* to B leads to increased robustness with respect to δE₁. For enzyme 2, the values are fixed at E₂ = 10 μm and . i, ; ii, ; iii, ; iv, ; v, , .

Figure 5.—

Saturation values for the two enzymes and the tendencies for robustness modification. (A) Frequency of cases with λ₁ < 0. (B) Frequency of cases with λ₂ < 0. Lighter areas indicate regions where a high proportion of increases in k_cati lead to an increase in robustness with respect to δE_i.

Figure 6.—

Alternative trajectories for attaining robustness with respect to changes at both the enz1 and enz2 loci.

Figure 7.—

Comparison of fixation-approach times for different phenotypes in the two-allele scenario. Each line represents pooled data from 32 trials. Fixation approach was scored when respective phenotype frequencies surpassed 0.95. Each labeled dot represents the median number of generations at which half of the trials had first gone above a frequency of 95% for the given kinetic phenotype. (A) Full linkage. (B) Free recombination. i, high E₁, high E₂, low k_cat1, low k_cat2; ii, high E₁, high E₂, high k_cat1, low k_cat2; iii, high E₁, high E₂, low k_cat1, high k_cat2; iv, high E₁, high E₂, high k_cat1, high k_cat2.

Figure 8.—

Selection for the high-k_cat1 kinetic phenotype in the two-allele scenario with full linkage. Dots show cumulative frequency. Bars show frequency in each bin of width 0.01. (A) Most of the increases in the high-k_cat1 phenotype occur when the frequency of the enz1wt/enz1mut heterozygote is <1%. (B) The likelihood of increases in the frequency of the high-k_cat1 phenotype is not affected by the frequency of the enz1wt/enz1wt, enz2wt/enz2wt, cat1mut/cat1mut, cat2mut/cat2mut genotype.

Figure 9.—

Evolutionary trajectories from 500 simulation trials of a continuum of alleles scenario. Horizontal axis m denotes number of mutations. Solid lines denote mean values and shaded areas denote standard deviations. (A) Evolution of the flux phenotype J (in millimolar per second). (B and C) Evolution of dominance with respect to mutations at the enz1 and enz2 loci (low D_i values signify dominance of the wild type). (D and E) Evolution of saturation values.